
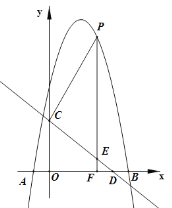
【题目】如图,抛物线![]() 与x轴交于A(-1,0),B(5,0)两点,直线
与x轴交于A(-1,0),B(5,0)两点,直线![]() 与y轴交于点C,与x轴交于点D。点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴与点F,交直线CD于点E。设点P的横坐标为m。
与y轴交于点C,与x轴交于点D。点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴与点F,交直线CD于点E。设点P的横坐标为m。
(1)求抛物线的解析式;
(2)若PF=5EF,求m的值.
科目:初中数学 来源: 题型:
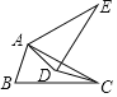
【题目】如图,在△ABC中,AC=BC,将△ABC绕点A逆时针旋转60°,得到△ADE,若AB=2,∠ACB=30°,则线段CD的长度为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
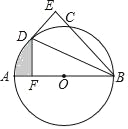
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
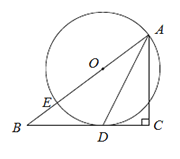
【题目】已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,连结AD.
(1)求证:AD是∠BAC的平分线;
(2)若AC=3,BC=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
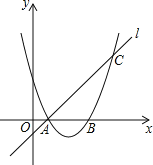
(1)求抛物线的解析式;
(2)设直线l与y轴交于点D,抛物线交y轴于点E,则△DBE的面积是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
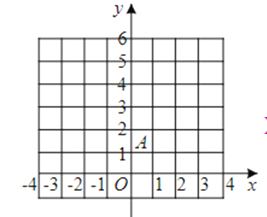
【题目】如图,在平面直角坐标系xoy中,点A的坐标为(0,1),取一点B(b,0),连接AB,作线段AB的垂直平分线![]() ,过点B作X轴的垂线
,过点B作X轴的垂线![]() ,记
,记![]() ,
,![]() 的交点为P。
的交点为P。
(1)当b=3时,在图1中补全图形(尺规作图,不写作法,保留作图痕迹)。
(2)小慧多次取不同数值b,得出相应的点P,并把这些点用平滑的曲线连接起来,发现:这些点P竟然在一条曲线L上。
①设点P的坐标为(x,y),试求y与x之间的关系式,并指出曲线L是哪种曲线。
②设点P到x轴,y轴的距离分别为![]() ,
,![]() ,求
,求![]() +
+![]() 的范围。当
的范围。当![]() +
+![]() =8时,求点P的坐标。
=8时,求点P的坐标。
③将曲线在直线y=2下方的部分沿直线y=2向上翻折,得到一条“W”形状的新曲线,若直线y=kx+3与这条“W”形状的新曲线有4个交点,直接写出k的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线y=﹣5x+5与x轴、y轴分别交于A,C两点,抛物线y=x2+bx+c经过A,C两点,与x轴交于另一点B.
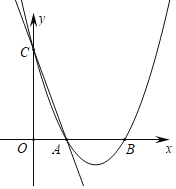
(1)求抛物线解析式及B点坐标;
(2)x2+bx+c≥﹣5x+5的解集 .
(3)若点M在第一象限内抛物线上一动点,连接MA、MB,当点M运动到某一位置时,△ABM面积为△ABC的面积的![]() 倍,求此时点M的坐标.
倍,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》“勾股”一章记载:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”译文:已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?(1丈=10尺,1尺=10寸)设长方形门的宽![]() 尺,可列方程为_______.
尺,可列方程为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小林准备进行如下操作试验:把一根长为![]() 的铁丝剪成两段,并把每一段各围成一个正方形.
的铁丝剪成两段,并把每一段各围成一个正方形.
(1)要使这两个正方形的面积之和等于![]() ,小林该怎么剪?
,小林该怎么剪?
(2)小峰对小林说:“这两个正方形的面积之和不可能等于![]() .”他的说法对吗?请说明理由.
.”他的说法对吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com