
【题目】如图1,等腰△ABC中,AB=AC,∠BAC=30°,AB边上的中垂线DE分别交AB,AC于点D、E,∠BAC的平分线交DE于点F.连接BF、CF、BE.
(1)求证:△BCF为等边三角形;
(2)猜想EF、EB、EC三条线段的关系,并说明理由;
(3)如图2,在BE的延长线上取一点M,连接AM,使AM=AB,连接MC并延长交AF的延长线于点M.求证:AN=MC.

【答案】(1)详见解析;(2)BE=EF+EC,理由详见解析;(3)详见解析.
【解析】
(1)先根据角平分线定义得:∠BAF=∠CAF=15°,根据等腰三角形性质得:∠ABC=
∠ACB=75°,计算∠FBC=60°,由中垂线的性质得:AF=BF,证明△BAF≌△CAF(SAS),
可得BF=CF,根据有一个角是60°的等腰三角形是等边三角形,可得结论;
(2)如图1,作辅助线,构建等边三角形EFG,证明△BFG≌△CFE,可得BG=EC,可得:
BE=BG+EG=EF+EC;
(3)如图2,设AE=x,分别计算∠CAM=90°,∠NAH=60°,∠ANH=30°,可得![]()
![]() ,可得结论.
,可得结论.
证明:(1)如图1,∵∠BAC=30°,AF平分∠BAC,
∴∠BAF=∠CAF=15°,
∵AB=AC,
∴∠ABC=∠ACB=75°,
∵DE是AB的中垂线,
∴AF=BF,
∴∠BAF=∠ABF=15°,
∴∠FBC=75°﹣15°=60°,
在△BAF和△CAF中,
∵ 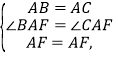
∴△BAF≌△CAF(SAS),
∴BF=CF,
∴△BCF是等边三角形;
(2)猜想:BE=EF+EC,
如图1,在BE上截取EF=FG,
∵DE是AB的中垂线,
∴AE=BE,
∴∠BED=∠AED=60°,
∴△FGE是等边三角形,
∴∠GFE=60°,EF=EG,
∵∠BFC=60°,
∴∠BFG=∠CFE,
在△BFG和△CFE中,
∵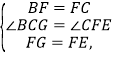
∴△BFG≌△CFE,
∴BG=EC,
∴BE=BG+EG=EF+EC;
(3)如图2,∵∠ABE=∠BAE=30°,
∴∠AEM=60°,
∵AB=AM,
∴∠ABE=∠AMB=30°,
∴∠EAM=90°,
设AE=x,则EM=2x,![]()
∵AB=AC=AM,
∴△ACM是等腰直角三角形,
∴![]()
∠AMC=45°,
过A作AH⊥MN于H,
∴△AMH是等腰直角三角形,
∴![]()
∵AC=AM,AH⊥CM,
∴∠CAH=45°,
∵∠NAC=![]() ∠BAC=15°,
∠BAC=15°,
∴∠NAH=15°+45°=60°,
∴∠ANH=30°,
∴![]()
∴AN=CM.


科目:初中数学 来源: 题型:
【题目】某届世界杯足球赛即将开幕,某媒体足球栏目从参加世界杯的球队中选出五支传统强队:意大利队、德国队、西班牙队、巴西队、阿根廷队,对哪支球队最有可能获得冠军进行了问卷调查,为了使调查结果有效,每位被调查者只能填写一份问卷,在问卷中必须选择这五支球队中的一队作为调查结果.从收集到的4800份有效问卷中随机抽取部分问卷进行统计,绘制了统计图表的一部分如下:
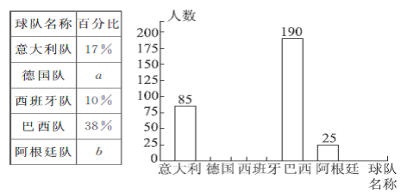
根据统计图提供的信息,解答下列问题:
(1)a= ,b= ;
(2)根据以上信息,请补全条形统计图;
(3)根据抽样调查结果,请你估计在提供有效问卷的这4800人中有多少人预测德国队最有可能获得冠军.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:善于思考的小军在解方程组![]() 时,采用了一种“整体代换”的解法,
时,采用了一种“整体代换”的解法,
解:将方程②变形:4x+10y+y=5即2(2x+5y)+y=5③,把方程①代入③得:2×3+y=5,y=﹣1,把y=﹣1代入①得x=4,所以,方程组的解为![]() .
.
请你解决以下问题:
(1)模仿小军的“整体代换”法解方程组![]() .
.
(2)已知x,y满足方程组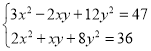 ,求x2+4y2﹣xy的值.
,求x2+4y2﹣xy的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PQ∥MN,A、B分别为直线MN、PQ上两点,且∠BAN=45°,若射线AM绕点A顺时针旋转至AN后立即回转,射线BQ绕点B逆时针旋转至BP后立即回转,两射线分别绕点A、点B不停地旋转,若射线AM转动的速度是a°/秒,射线BQ转动的速度是b°/秒,且a、b满足|a﹣5|+(b﹣1)2=0.(友情提醒:钟表指针走动的方向为顺时针方向)
(1)a= ,b= ;
(2)若射线AM、射线BQ同时旋转,问至少旋转多少秒时,射线AM、射线BQ互相垂直.
(3)若射线AM绕点A顺时针先转动18秒,射线BQ才开始绕点B逆时针旋转,在射线BQ到达BA之前,问射线AM再转动多少秒时,射线AM、射线BQ互相平行?

查看答案和解析>>
科目:初中数学 来源: 题型:
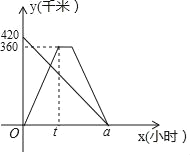
【题目】甲、乙两车分别从相距480千米的A、B两地相向而行,乙车出发1小时后甲车出发,并以各自的速度匀速行驶,途经C地,甲车到达C地停留1小时,因有事按原路原速返回A地,乙车从B地直达A地,两车同时到达A地.甲、乙两车与A地的距离y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)图中数据420的含义正确的有 ;(填写序号)
①乙车出发时与A地的距离;
②甲车出发时与B地的距离;
③甲车出发时,乙车与A地的距离;
(2)乙车的速度是 千米/时,a= 小时;甲车的速度是 千米/时,t= 小时.
(3)在甲车到达C地之前,两车能否相遇?若能相遇,请求出甲车行驶的时间;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD=BC=12,AB=CD,BD=15,点E从D点出发,以每秒4个单位的速度沿D→A→D匀速移动,点F从点C出发,以每秒1个单位的速度沿CB向点B作匀速移动,点G从点B出发沿BD向点D匀速移动,三个点同时出发,当有一个点到达终点时,其余两点也随之停止运动,假设移动时间为t秒.

(1)试说明:AD∥BC;
(2)在移动过程中,小明发现有△DEG与△BFG全等的情况出现,请你探究这样的情况会出现几次?并分别求出此时的移动时间t和G点的移动距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路上有![]() 、
、![]() 两地,甲乙两人同时出发,甲骑自行车从
两地,甲乙两人同时出发,甲骑自行车从![]() 地到
地到![]() 地,乙骑自行车从
地,乙骑自行车从![]() 地到
地到![]() 地,到达
地,到达![]() 地后立即按原路返回
地后立即按原路返回![]() 地.如图是甲、乙两人离
地.如图是甲、乙两人离![]() 地的距离
地的距离![]() 与行驶时间
与行驶时间![]() 之间的函数图象,下列说法中①
之间的函数图象,下列说法中①![]() 、
、![]() 两地相距30千米;②甲的速度为15千米/时;③点
两地相距30千米;②甲的速度为15千米/时;③点![]() 的坐标为(
的坐标为(![]() ,20);④当甲、乙两人相距10千米时,他们的行驶时间是
,20);④当甲、乙两人相距10千米时,他们的行驶时间是![]() 小时或
小时或![]() 小时. 正确的个数为( )
小时. 正确的个数为( )

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com