
【题目】2019年双“十一”期间,天猫商场某书店制定了促销方案:若一次性购书超过300元,其中300元按九五折优惠,超过300元的部分按八折优惠.
(1)设一次性购买的书籍原价是a元,当a超过300时,实际付款 元;(用含a的代数式表示,并化简)
(2)若小明购书时一次性付款365元,则所购书籍的原价是多少元?
(3)小冬在促销期间先后两次下单购买书籍,两次所购书籍的原价之和为600元(第一次所购书籍的原价高于第二次),两次实际共付款555元,则小冬两次购物所购书籍的原价分别是多少元?
【答案】(1)![]() ;(2)400;(3)450元和150元
;(2)400;(3)450元和150元
【解析】
(1)根据题干中的优惠方案用代数式表示即可;
(2)设购书的原价为b元,根据题意列出方程,解之即可;
(3)设第一次购买书籍为c元,根据第一次所购书籍的原价高于第二次判断出第一次原价大于300,第二次原价小于300,可列方程求解.
解:(1)(a-300)×80%+300×95%=![]() ;
;
(2)设购书的原价为b元,因为365>300,所以b>300,
则可得方程:(b-300)×80%+300×95%=365
解得b=400,
答:所购书籍的原价是400元;
(3)设第一次购买书籍为c元,根据题意:c>300,即第一次原价大于300,第二次原价小于300,根据(1)可列方程为
0.8c+45+(600-c)=555
解得:c=450,
600-450=150(元),
答:小冬两次购物所购书籍的原价分别是450元、150元.


科目:初中数学 来源: 题型:
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.下列结论正确的个数是( )
(1)t=5时,s=150;(2)t=35时,s=450;(3)甲的速度是30米/分;(4)t=12.5时,s=0.

A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
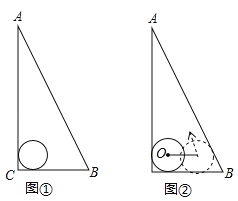
【题目】如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】结合数轴与绝对值的知识回答下列问题:
(1)数轴上表示4和1的两点之间的距离是 ;表示-3和2两点之间的距离是 ;一般地,数轴上表示数m和数n的两点之间的距离等于![]() .如果表示数
.如果表示数![]() 和-2的两点之间的距离是3,那么
和-2的两点之间的距离是3,那么![]() = ;
= ;
(2)若数轴上表示数![]() 的点位于-4与2之间,求
的点位于-4与2之间,求![]() +
+![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.(以下计算结果精确到0.1m)
(1)求小明此时与地面的垂直距离CD的值;
(2)小明的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(sin15°≈0.2588,cos15°≈0.9659 ,tan≈.0.2677 )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a≠0)的部分图像,其中点A(-1,0)是x轴上的一个交点,点C是y轴上的交点.
(1)若过点A的直线l与这个二次函数的图像的另一个交点为D,与该图像的对称轴交于点E,与y轴交于点F,且DE=EF=FA.
①求![]() 的值;
的值;
②设这个二次函数图像的顶点为P,问:以DF为直径的圆能否经过点P?若能,请求出此时二次函数的关系式;若不能,请说明理由.
(2)若点C坐标为(0,-1),设S=a+b+c ,求S的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.

(2)利用(1)中所得到的结论,解决下面的问题: 已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=12,AD=4,BC=9,点P是AB上一动点.若△PAD与△PBC是相似三角形,则满足条件的点P的个数有( )
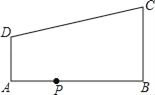
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com