
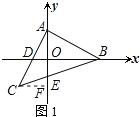
【题目】等腰Rt△ABC中,∠BAC=90°,点A、点B分别是y轴、x轴上的两个动点,点C在第三象限,直角边AC交x轴于点D,斜边BC交y轴于点E.
(1)若A(0,1),B(2,0),画出图形并求C点的坐标;
(2)若点D恰为AC中点时,连接DE,画出图形,判断∠ADB和∠CDE大小关系,说明理由.
【答案】(1)作图见解析,C(﹣1,﹣1);(2)∠ADB=∠CDE.理由见解析.
【解析】
(1)过点C作CF⊥y轴于点F通过证明△ACF≌△BAO得CF=OA=1,AF=OB=2,求得OF的值,就可以求出C的坐标;
(2)过点C作CG⊥AC交y轴于点G,先证明△ACG≌△BAD就可以得出CG=AD=CD,∠DCE=∠GCE=45°,再证明△DCE≌△GCE就可以得出结论.
解:(1)过点C作CF⊥y轴于点F,如图1所示:
 ,
,
∴∠AFC=90°,
∴∠CAF+∠ACF=90°.
∵△ABC是等腰直角三角形,∠BAC=90°,
∴AC=AB,∠CAF+∠BAO=90°,∠AFC=∠BAC,
∴∠ACF=∠BAO.
在△ACF和△BAO中,
∵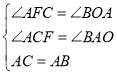 ,
,
∴△ACF≌△BAO(AAS),
∴CF=OA=1,AF=OB=2,
∴OF=1,
∴C(﹣1,﹣1);
(2)∠ADB=∠CDE.理由如下:
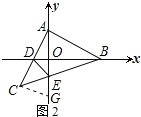
证明:过点C作CG⊥AC交y轴于点G,如图2所示:
 ,
,
∴∠ACG=∠BAC=90°,
∴∠AGC+∠GAC=90°.
∵∠CAG+∠BAO=90°,
∴∠AGC=∠BAO.
∵∠ADO+∠DAO=90°,∠DAO+∠BAO=90°,
∴∠ADO=∠BAO,
∴∠AGC=∠ADO.
在△ACG和△BAD中,
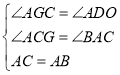 ,
,
∴△ACG≌△BAD(AAS),
∴CG=AD=CD.
∵∠ACB=∠ABC=45°,
∴∠DCE=∠GCE=45°,
在△DCE和△GCE中,
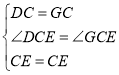 ,
,
∴△DCE≌△GCE(SAS),
∴∠CDE=∠CGE,
∴∠ADB=∠CDE.


科目:初中数学 来源: 题型:
【题目】计算或解方程:
(1)计算下列各题
①(π﹣3.14)0+(﹣![]() )2﹣3﹣2;
)2﹣3﹣2;
②(3a﹣1)2﹣(3a﹣2)(3a+4);
③(12a5b7﹣8a4b6﹣4a4b2)÷(﹣2a2b)2;
(2)解分式方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=60°,∠BAC的平分线AD与边BC的垂直平分线相交于点D,DE⊥AB交AB的延长线于点E,DF⊥AC于点F,现有下列结论:①DE=DF;②DE+DF=AD;③AM平分∠ADF;④AB+AC=2AE;其中正确的有( )

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
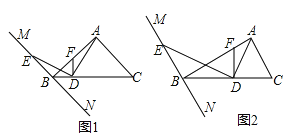
【题目】在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.
(1)如图①,当∠ABC=45°时,求证:AD=DE;理由;
(2)如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;
(3)当∠ABC=α时,请直接写出线段AD与DE的数量关系.(用含α的三角函数表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
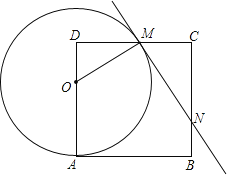
(1)图中是否存在与△ODM相似的三角形,若存在,请找出并给予证明;
(2)设DM=x,OA=R,求R关于x的函数关系式;
(3)在动点O逐渐向点D运动(OA逐渐增大)的过程中,△CMN的周长如何变化?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
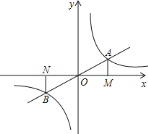
【题目】如图,正比例函数![]() 的图象与反比例函数
的图象与反比例函数![]() 在第一象限的图象交于
在第一象限的图象交于![]() 点,过
点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,已知
,已知![]() 的面积为
的面积为![]() .
.
![]() 求反比例函数的解析式;
求反比例函数的解析式;
![]() 如图,点
如图,点![]() 为反比例函数在第三象限图象上的点,过
为反比例函数在第三象限图象上的点,过![]() 点作
点作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,过顶点
,过顶点![]() 作射线
作射线![]() .
.
(1)当射线![]() 在
在![]() 外部时,如图①,点
外部时,如图①,点![]() 在射线
在射线![]() 上,连结
上,连结![]() 、
、![]() ,已知
,已知![]() ,
,![]() ,
,![]() (
(![]() ).
).
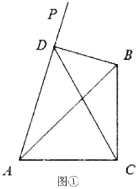
①试证明![]() 是直角三角形;
是直角三角形;
②求线段![]() 的长.(用含
的长.(用含![]() 的代数式表示)
的代数式表示)
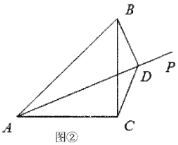
(2)当射线![]() 在
在![]() 内部时,如图②,过点
内部时,如图②,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,请写出线段
,请写出线段![]() 、
、![]() 、
、![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC中,AB=AC=BC=10厘米,M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度是1厘米/秒的速度,点N的速度是2厘米/秒,当点N第一次到达B点时,M、N同时停止运动.
(1)M、N同时运动几秒后,M、N两点重合?
(2)M、N同时运动几秒后,可得等边三角形△AMN?
(3)M、N在BC边上运动时,能否得到以MN为底边的等腰△AMN,如果存在,请求出此时M、N运动的时间?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com