
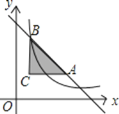
【题目】如图,过点C(1,2)分别作x轴、y轴的平行线,交直线y=﹣x+6于A、B两点,若反比例函数![]() (x>0)的图象与△ABC有公共点,则k的取值范围是________.
(x>0)的图象与△ABC有公共点,则k的取值范围是________.
【答案】![]()
【解析】
先求出点A、B的坐标,根据反比例函数系数的几何意义可知,当反比例函数图象与△ABC相交于点C时k的取值最小,当与线段AB相交时,k能取到最大值,根据直线y=-x+6,设交点为(x,-x+6)时k值最大,然后列式利用二次函数的最值问题解答即可得解.
:∵点C(1,2),BC∥y轴,AC∥x轴,
∴当x=1时,y=-1+6=5,
当y=2时,-x+6=2,解得x=4,
∴点A、B的坐标分别为A(4,2),B(1,5),
根据反比例函数系数的几何意义,当反比例函数与点C相交时,k=1×2=2最小,
设反比例函数与线段AB相交于点(x,-x+6)时k值最大,
则k=x(-x+6)=-x2+6x=-(x-3)2+9,
∵1≤x≤4,
∴当x=3时,k值最大,
此时交点坐标为(3,3),
因此,k的取值范围是2≤k≤9.
故答案为:2≤k≤9.


科目:初中数学 来源: 题型:
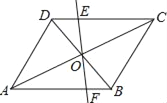
【题目】如图,点O是平行四边形ABCD的对称中心,将直线DB绕点O顺时针方向旋转,交DC、AB于点E、F.
(1)证明:△DEO≌△BFO;
(2)若DB=2,AD=1,AB=![]() ,当DB绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
,当DB绕点O顺时针方向旋转45°时,判断四边形AECF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
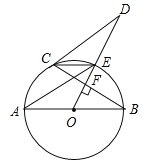
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知线段a,P为线段a上任意一点,已知图形M,Q为图形M上任意一点,当P,Q两点间的距离最小时,将此时PQ的长度称为图形M与线段a的近点距;当P,Q两点间的距离最大时,将此时PQ的长度称为图形M与线段a的远点距.

根据阅读材料解决下列问题:
如图1,在平面直角坐标系xOy中,点A的坐标为(﹣2,﹣2),正方形ABCD的对称中心为原点O.
(1)线段AB与线段CD的近点距是 ,远点距是 .
(2)如图2,直线y=﹣x+6与x轴,y轴分别交于点E,F,则线段EF和正方形ABCD的近点距是 ,远点距是 ;
(3)直线y=x+b(b≠0)与x轴,y轴分别交于点R,S,线段RS与正方形ABCD的近距点是![]() ,则b的值是 ;
,则b的值是 ;
(4)在平面直角坐标系xOy中,有一个矩形GHMN,若此矩形至少有一个顶点在以O为圆心1为半径的圆上,其余各点可能在圆上或圆内,将正方形ABCD绕点O旋转一周,在旋转过程中,它与矩形GHMN的近点距的最小值是 ,远点距的最大值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
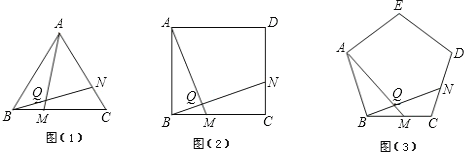
【题目】(1)如图(1),已知△ABC为正三角形,点M是BC上一点,点N是AC上一点,AM、BN相交于点Q,BM=CN.求出∠BQM的度数;
(2)将(1)中的“正△ABC”分别改为正方形ABCD、正五边形ABCDE、…正n边形ABCD…,“点N是AC上一点”改为点N是CD上一点,其余条件不变,分别推断出∠BQM等于多少度,将结论填入下表:
正多边形 | 正方形 | 正五边形 | …… | 正n边形 |
∠BQM的度数 |
|
| …… |
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们不妨把横坐标与纵坐标相等的点称为梦之点,例如,点(1,1),(﹣ 2,﹣ 2),(![]() ,
,![]() ),…,都是梦之点,显然梦之点有无数个.
),…,都是梦之点,显然梦之点有无数个.
(1)若点 P(2,b)是反比例函数![]() (n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(n 为常数,n ≠ 0) 的图象上的梦之点,求这个反比例函数解析式;
(2)⊙O 的半径是![]() ,
,
①求出⊙O上的所有梦之点的坐标;
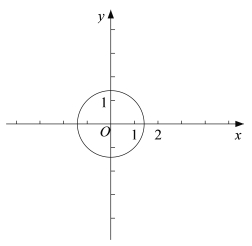
②已知点 M(m,3),点 Q 是(1)中反比例函数![]() 图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,∠OAQ=45°.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
图象上异于点 P 的梦之点,过点Q 的直线 l 与 y 轴交于点 A,∠OAQ=45°.若在⊙ O 上存在一点 N,使得直线 MN ∥ l或 MN ⊥ l,求出 m 的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
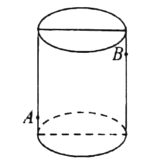
【题目】有一个圆柱形玻璃杯高![]() ,底面周长为
,底面周长为![]() ,有一只蚂蚁在一侧距下底
,有一只蚂蚁在一侧距下底![]() 的外侧
的外侧![]() 点,与点
点,与点![]() 正对的容器内侧距下底
正对的容器内侧距下底![]() 的
的![]() 点处有一饭粒,蚂蚁想吃
点处有一饭粒,蚂蚁想吃![]() 处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________
处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有甲、乙两个不透明的布袋,甲袋中有2个完全相同的小球,分别标有数字0和-2;乙袋中有3个完全相同的小球,分别标有数字-2,0和1,小明从甲袋中随机取出1个小球,记录标有的数字为x,再从乙袋中随机取出1个小球,记录标有的数字为y,这样确定了点Q的坐标(x,y).
(1)写出点Q所有可能的坐标;
(2)求点Q在x轴上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com