
分析 首先根据-1<b<0,0<a<1,判断出-b>b,0<b2<1,0<a2<1,然后比较大小,判断出在代数式a-b,a+b,a+b2,a2+b中,对任意的a,b,对应的代数式的值最大的是哪个算式即可.
解答 解:∵-1<b<0,
∴-b>b,0<b2<1,
∴a-b>a+b,a-b>a+b2;
又∵0<a<1,
∴0<a2<1,
∴a-b>a2+b;
综上,可得
在代数式a-b,a+b,a+b2,a2+b中,对任意的a,b,对应的代数式的值最大的是a-b.
故答案为:a-b.
点评 此题主要考查了代数式的求值问题,以及代数式的值的大小比较,要熟练掌握,解答此题的关键是要明确:∴-b>b,0<b2<1,0<a2<1.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
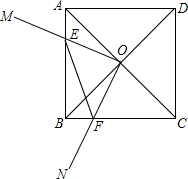 如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.
如图,正方形ABCD的对角线AC、BD的交点为O,以O为端点引两条互相垂直的射线OM、ON,分别交边AB、BC于点E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com