
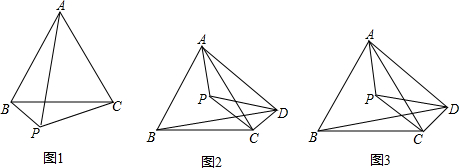
分析 (1)要证明PA=PB+PC,只需要作出合适的辅助线延长BP至点E,使得PE=PC,连接CE,证明△ACP≌△BCE即可;
(2)要证明PA+PD+PC>BD,只需要作辅助线延长DP到M使得PM=PA,连接AM、BM,画出相应的图形,根据三角形两边之和大于第三边即可证明结论;
(3)要求$\frac{AC}{BD}$的比值,只要求出AC、BD的值即可,要求它们的值,根据(2)中得到的结论和题意可以求得它们的长,本题得以解决.
解答 (1)证明:延长BP至点E,使得PE=PC,连接CE,如下图1所示,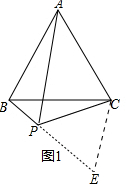
∵∠BPC=120°,PE=PC,
∴∠CPE=60°,
∴△CPE为等边三角形,
∴CP=PE=CE,∠PCE=60°,
∵△ABC是等边三角形,
∴AC=BC,∠BCA=60°,
∴∠ACB=∠ECP,
∴∠ACB+∠BCP=∠ECP+∠BCP,
即:∠ACP=∠BCE,
在△ACP和△BCE中
$\left\{\begin{array}{l}{AC=BC}\\{∠ACP=∠BCE}\\{PE=PC}\end{array}\right.$
∴△ACP≌△BCE(SAS)
∴AP=BE,
∵BE=BP+PE=BP+PC,
∴PA=PB+PC;
(2)证明:延长DP到M使得PM=PA,连接AM、BM,如下图2所示,
∵∠APD=120°,PM=PA,
∴∠APM=60°,
∴△APM是等边三角形,
∴AM=AP,∠PAM=60°,
∴DM=PD+PA,
∵△ABC是等边三角形,
∴AB=AC,∠BAC=60°,
∴∠MAP=∠BAC,
∴∠MAP-∠BAP=∠BAC-∠BAP,
即∠MAB=∠PAC,
在△AMB和△APC中,
$\left\{\begin{array}{l}{AM=AP}\\{∠MAB=∠PAC}\\{AB=AC}\end{array}\right.$
∴△AMB≌△APC(SAS)
∴BM=PC,
∵在△BDM中,DM+BM>BD,DM=PD+PA,
∴PA+PD+PC>BD.
(3)解:延长DP到M使得PM=PA,连接AM、BM,延长CP交AM的于点N,如下图3所示,
由(2)可知,△AMP为等边三角形,BM=PC,
∵∠APD=120°,∠APC=150°,PA=4,PC=5,PD=8,
∴∠CPD=∠APC-∠APD=30°,
∴∠MPN=30°,
∴PN⊥AM,
∵PA=4,PC=5,
∴AN=2,NP=$2\sqrt{3}$,
∴CN=$5+2\sqrt{3}$,
∴AC=$\sqrt{A{N}^{2}+C{N}^{2}}=\sqrt{{2}^{2}+(5+2\sqrt{3})^{2}}$=$\sqrt{41+20\sqrt{3}}$,
∵∠AMB=∠APC=150°,∠AMP=60°,
∴∠BMD=90°,
∵DM=MP+PD=4+8=12,BM=5,
∴BD=$\sqrt{B{M}^{2}+M{D}^{2}}=\sqrt{{5}^{2}+1{2}^{2}}=13$,
∴$\frac{AC}{BD}=\frac{\sqrt{41+20\sqrt{3}}}{13}$,
故答案为:$\frac{\sqrt{41+20\sqrt{3}}}{13}$.
点评 本题考查几何综合变化、三角形两边之和大于第三边、构造三角形,直角三角形的相关知识、等边三角形的性质,解题的关键是明确题意,做出合适的辅助线,画出相应的图形,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
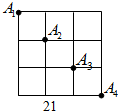 如图,点A1、A2、A3、A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有6种.
如图,点A1、A2、A3、A4是某市正方形道路网的部分交汇点,且它们都位于同一对角线上.某人从点A1出发,规定向右或向下行走,那么到达点A3的走法共有6种.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com