
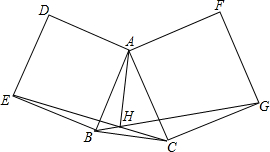
 在△ABC的边AB,AC向外作正方形ABED,ACGF,BG、CE相交于H.求证:AH⊥BC.
在△ABC的边AB,AC向外作正方形ABED,ACGF,BG、CE相交于H.求证:AH⊥BC. 分析 过A作AD⊥BC,延长DA到K,使AK=BC,连接KB,KC,分别交CE,BG于M,N,由于∠KAF+∠DAB=90°,∠ABD+∠DAB=90°,得到∠KAF=∠ABD,推出∠KAB=∠BCE,由∠AKB+∠KBD=90°,得到∠BCE+∠KBD=90°,于是得到∠BCM+∠MBC=90°,根据垂直的定义得到CE⊥KB,同理BG⊥KC推出AD必过O点,于是得到结论.
解答 解: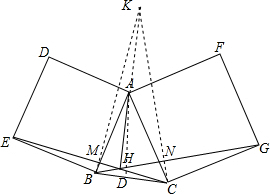 过A作AD⊥BC,延长DA到K,使AK=BC,连接KB,KC,分别交CE,BG于M,N,
过A作AD⊥BC,延长DA到K,使AK=BC,连接KB,KC,分别交CE,BG于M,N,
∵∠KAF+∠DAB=90°,∠ABD+∠DAB=90°,
∴∠KAF=∠ABD,
∴∠KAB=∠BCE,
∵∠AKB+∠KBD=90°,
∴∠BCE+∠KBD=90°,
∴∠BCM+∠MBC=90°,
∴CE⊥KB,同理BG⊥KC,
∴KD.CM,BN是△KBC的三条高,它们交于O,
∴AD必过O点,
∴AO⊥BC.
点评 本题考查了正方形的性质,余角的性质,正确的作出辅助线是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
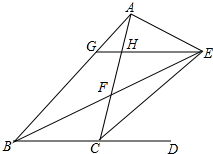 如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论;
如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论;| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
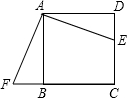 如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )
如图,E是正方形ABCD的边DC上一点,过点A作FA=AE交CB的延长线于点F,若AB=4,则四边形AFCE的面积是( )| A. | 4 | B. | 8 | C. | 16 | D. | 无法计算 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB=16cm,点D为射线AC上一点,且AD=20cm,点E是平面上任一点,且BE=3AE.
如图,AB=16cm,点D为射线AC上一点,且AD=20cm,点E是平面上任一点,且BE=3AE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com