
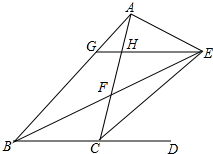
 如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论;
如图,△ABC内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,有以下结论;| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据角平分线定义得出∠ABE=∠CBE,根据平行线性质得出∠CBE=∠BEG,从而得出∠ABE=∠BEG,由等腰三角形的判定定理即可得到结论;
②根据相似三角形的判定定理得到两个三角形相似,不能得出全等;
③由于E是两条角平分线的交点,根据角平分线的性质可得出点E到BA、AC、BC和距离相等,从而得出AE为∠BAC外角平分线这个重要结论,再利用三角形内角和性质与外角性质进行角度的推导即可轻松得出结论.
④根据∠AEC=180-x-z,于是得到∠AEC=180-(y+90°),推出y+∠AEC=90°,即可得到结论;
⑤由BG=GE,CH=EH,于是得到BG-CH=GE-EH=GH.即可得到结论.
解答 解:①∵BE平分∠ABC,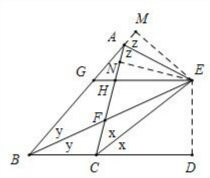 π
π
∴∠ABE=∠CBE,
∵GE∥BC,
∴∠CBE=∠GEB,
∴∠ABE=∠GEB,
∴BG=GE,故①正确.
同理CH=HE.
②△HEF与△CBF只有两个角是相等的,能得出相似,但不含相等的边,所有不能得出全等的结论,故②错误.
③过点E作EN⊥AC于N,ED⊥BC于D,EM⊥BA于M,如图,
∵BE平分∠ABC,
∴EM=ED,
∵CE平分∠ACD,
∴EN=ED,
∴EN=EM,
∴AE平分∠CAM,
设∠ACE=∠DCE=x,∠ABE=∠CBE=y,∠MAE=∠CAE=z,如图,
则∠BAC=180°-2z,∠ACB=180-2x,
∵∠ABC+∠ACB+∠BAC=180°,
∴2y+180°-2z+180°-2x=180°,
∴x+z=y+90°,
∵z=y+∠AEB,
∴x+y+∠AEB=y+90°,
∴x+∠AEB=90°,
即∠ACE+∠AEB=90°,故③正确.
④∵∠AEC=180-x-z,
∴∠AEC=180-(y+90°),
∴y+∠AEC=90°,
即∠ABE+∠AEC=90°,
故④正确.
⑤∵BG=GE,CH=EH,
∴BG-CH=GE-EH=GH.
故⑤正确.
综上,①③④⑤正确,共4个.
故选D.
点评 本题考查了平行线的性质,角平分线的定义,角平分线的性质与判定,等腰三角形的判定,三角形内角和定理、三角形外角性质等多个知识点,难度中等.判断出AE是∠BAC外角平分线是关键,事实上,点E就是△ABC的旁心.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
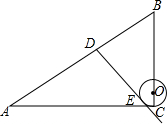 如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )
如图,在Rt△ABC中,∠C=90°,AC=8,AB=10,点O为BC上的点,⊙O的半径OC=1,点D是AB边上的动点,过点D作⊙O的一条切线DE(点E为切点),则线段DE的最小值为( )| A. | $3\sqrt{2}-1$ | B. | $\sqrt{15}-1$ | C. | $\sqrt{15}$ | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com