
【题目】类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
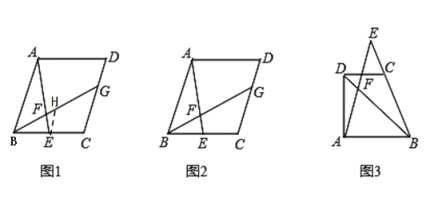
原题:如图1,在平行四边形ABCD中,点E是BC的中点,点F是线段AE上一点,BF的延长线交射线CD于点G.若![]() ,求
,求![]() 的值.
的值.
(1)尝试探究
在图1中,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是 ,CG和EH的数量关系是 ,![]() 的值是 .
的值是 .
(2)类比延伸
如图2,在原题的条件下,若![]() 求
求![]() 的值(用含有m的代数式表示).
的值(用含有m的代数式表示).
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC的延长线上的一点,AE和BD相交于点F. 若![]() ,求
,求![]() 的值.
的值.
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
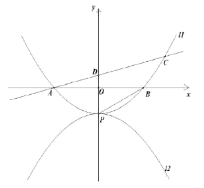
【题目】已知抛物线![]() :
:![]() 的项点为
的项点为![]() ,交
,交![]() 轴于
轴于![]() 、
、![]() 两点(
两点(![]() 点在
点在![]() 点左侧),且
点左侧),且![]() .
.
(1)求抛物线![]() 的函数解析式;
的函数解析式;
(2)过点![]() 的直线交抛物线于点
的直线交抛物线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,若
,若![]() 的面积被
的面积被![]() 轴分为1: 4两个部分,求直线
轴分为1: 4两个部分,求直线![]() 的解析式;
的解析式;
(3)在(2)的情况下,将抛物线![]() 绕点
绕点![]() 逆时针旋转180°得到抛物线
逆时针旋转180°得到抛物线![]() ,点
,点![]() 为抛物线
为抛物线![]() 上一点,当点
上一点,当点![]() 的横坐标为何值时,
的横坐标为何值时,![]() 为直角三角形?
为直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据市场调查,天猫超市在销售一种进价为每件40元的护眼台灯中发现:每月销售量![]() (件)与销售单价
(件)与销售单价![]() (元)之间的函数关系如图所示.
(元)之间的函数关系如图所示.
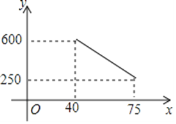
(1)当销售单价定为50元时,求每月的销售件数;
(2)设每月获得利润为![]() (元),求每月获得利润
(元),求每月获得利润![]() (元)关于销售单价
(元)关于销售单价![]() (元)的函数解析式;
(元)的函数解析式;
(3)由于市场竞争激烈,这种护眼灯的销售单价不得高于75元,如果要每月获得的利润不低于8000元,那么每月的成本最少需要多少元?(成本=进价×销售量).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的箱子里有四张外形相同的卡片卡片上分别标有数字﹣1,1,3,5.摸出一张后,记下数字,再放回,摇匀后再摸出一张,记下数字.以第一次得到的放字为横坐标,第二次得到的数字为纵坐标,得到一个点则这个点.恰好在直线y=﹣x+4上的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
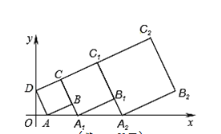
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交x轴于点
交x轴于点![]() ,作正方形
,作正方形![]() …按这样的规律进行下去,第2019个正方形的面积为( )
…按这样的规律进行下去,第2019个正方形的面积为( )
A.![]() B.
B.![]()
C.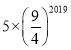 D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
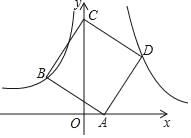
【题目】如图,正方形ABCD的顶点A在x轴的正半轴上,顶点C在y轴的正半轴上,点B在双曲线![]() (x<0)上,点D在双曲线
(x<0)上,点D在双曲线![]() (x>0)上,点D的坐标是 (3,3)
(x>0)上,点D的坐标是 (3,3)
(1)求k的值;
(2)求点A和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于![]() BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
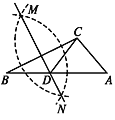
A.90°B.95°C.105°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=2AC,D,E,F分别为BC,AC,AB边上的点,BF=3AF,∠DFE=90°,若△BDF与△FEA的面积比为3:2,则△CDE与△DEF的面积比为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com