
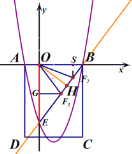
ЁОЬтФПЁПШчЭМЂйОиаЮABCDдкзјБъЯЕжаЕФЮЛжУШчЭМЫљЪОЃЌOBЃН3OAЃН3ЃЌBCЃН5ЃЌНЋЯпЖЮBCШЦЕуBа§зЊЃЌЪЙЕуCТфдкyжсИКАыжсЩЯЕФЕуEДІЃЌХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉОЙ§AЁЂBЁЂCШ§ЕуЃЎ
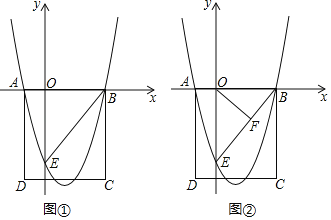
ЃЈ1ЃЉЧѓХзЮяЯпyЃНax2+bx+cЃЈaЁй0ЃЉЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌFЪЧжБЯпBEЩЯвЛЖЏЕуЃЎ
ЂйШчЭМЂкЃЌШєOFЁЭBEЃЌжБЯпPQЁЮOFНЛжБЯпBEгкЕуQЃЌШєвдPЁЂQЁЂFЁЂOЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓЕуPЕФКсзјБъЃЛ
ЂкШєжБЯпOFгыжБЯпBEЕФМаНЧЕШгкЁЯBEOЕФ2БЖЃЌЧыжБНгаДГіЕуFЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЂйЗћКЯЬѕМўЕФЕуPЕФКсзјБъЪЧ
ЃЛЃЈ2ЃЉЂйЗћКЯЬѕМўЕФЕуPЕФКсзјБъЪЧ![]() ЃЌ
ЃЌ![]() ЃЛЂкЗћКЯЬѕМўЕФЕуFЕФзјБъЪЧ(
ЃЛЂкЗћКЯЬѕМўЕФЕуFЕФзјБъЪЧ(![]() ,-2)ЃЌЃЈ
,-2)ЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ.
ЃЉ.
ЁОНтЮіЁП
(1)ЯШЧѓГіOEЕФГЄЃЌШЛКѓПЩЕУЕуAЁЂBЁЂEЕФзјБъЃЌДњШыПЩЕУХзЮяЯпЕФНтЮіЪНЃЛ
(2)ЂйШчЭМЃЌЙ§ЕуPзїжБЯпMNЁЭ![]() жсгкЕуM.НЛжБЯпBEгкЕуN,ЯШЧѓГіBEЕФНтЮіЪНЃЌШЛКѓдйЧѓГіЁїPNQЁеЁїOFE,ЗжБ№МЦЫуГіЕуPдкxжсЕФЩЯЗНКЭЕуPдкxжсЕФЯТЗНЕФКсзјБъжЕМДПЩНтД№
жсгкЕуM.НЛжБЯпBEгкЕуN,ЯШЧѓГіBEЕФНтЮіЪНЃЌШЛКѓдйЧѓГіЁїPNQЁеЁїOFE,ЗжБ№МЦЫуГіЕуPдкxжсЕФЩЯЗНКЭЕуPдкxжсЕФЯТЗНЕФКсзјБъжЕМДПЩНтД№
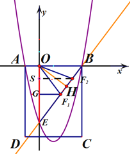
ЂкШчЭМЃЌзїOEЕФДЙжБЦНЗжЯпНЛBEгкЕу![]() ,зїOHЁЭBEгкЕуЃЌдкЯпBEЩЯзї
,зїOHЁЭBEгкЕуЃЌдкЯпBEЩЯзї![]() ЙигкЕуHЕФЖдГЦЕу
ЙигкЕуHЕФЖдГЦЕу![]() ЃЌЧѓГі
ЃЌЧѓГі![]() МДПЩЧѓГі
МДПЩЧѓГі![]() ЕФзјБъЃЛзї
ЕФзјБъЃЛзї![]() жсгкЕуS,ЭЈЙ§НтжБНЧШ§НЧаЮ
жсгкЕуS,ЭЈЙ§НтжБНЧШ§НЧаЮ![]() ,МДПЩЧѓГі
,МДПЩЧѓГі![]() ЕФзјБъМДПЩНтД№.
ЕФзјБъМДПЩНтД№.
(1) гЩЬтвтжЊЃЌOA=1,OB=3,BC=BE=5,
ЁпЁЯBOE=90,ЁрOE=![]() ,
,
ЁрA(-1,0),B(3,0),E(0,-4),
Ёр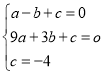 ЃЌНтжЎЕУ
ЃЌНтжЎЕУ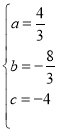 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЙ§ЕуPзїжБЯпMNЁЭ![]() жсгкЕуM.НЛжБЯпBEгкЕуN,
жсгкЕуM.НЛжБЯпBEгкЕуN,
ЁпжБЯпBEОЙ§ЕуB(3,0),E(0,-4)ЃЌ
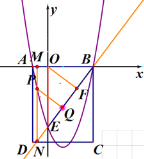
гУД§ЖЈЯЕЪ§ЗЈПЩЧѓжБЯпBEЕФНтЮіЪНЮЊ![]()
ЁпPQЁЮOF,OFЁЭBE,ЁрPQЁЭBE,
ЁпЫФБпаЮPQFOЮЊЦНааЫФБпаЮЃЌЁрPQ=FO=![]()
ЁпMNЁЮOE,ЁрЁЯOEF=ЁЯPNQ,ЁрЁїPNQЁеЁїOFE,
ЁрPN=OE=4,
ЩшЕуPЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌдђЕуQЕФзјБъЪЧЃЈ
ЃЉЃЌдђЕуQЕФзјБъЪЧЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Ёр ЕБЕуPдк![]() жсЕФЯТЗНЃЌPN=NM-PM=4 ,
жсЕФЯТЗНЃЌPN=NM-PM=4 ,
МД ![]() ЃЌ
ЃЌ
НтжЎЕУЃЌ![]() ЃЌ
ЃЌ![]() ЃЈЩсШЅЃЉЃЌ
ЃЈЩсШЅЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
ЕБЕуPдк![]() жсЕФЩЯЗНЃЌЭЌРэПЩЕУ
жсЕФЩЯЗНЃЌЭЌРэПЩЕУ![]() ЃЌ
ЃЌ
ЁрЗћКЯЬѕМўЕФЕуPЕФКсзјБъЪЧ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЂкзїOEЕФДЙжБЦНЗжЯпНЛBEгкЕу![]() ,зїOHЁЭBEгкЕуЃЌдкЯпBEЩЯзї
,зїOHЁЭBEгкЕуЃЌдкЯпBEЩЯзї![]() ЙигкЕуHЕФЖдГЦЕу
ЙигкЕуHЕФЖдГЦЕу![]() ,дђ
,дђ![]() ,
,
Ёп![]() ЃЌ
ЃЌ![]() ,Ёр
,Ёр![]() ,
,
Ёр![]() ,Ёр
,Ёр![]() (
(![]() ,-2);
,-2);
ЩшЕу![]() ЕФзјБъЪЧЃЈ
ЕФзјБъЪЧЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌзї
ЃЉЃЌзї![]() жсгкЕуS,
жсгкЕуS,
дђOS=![]() ЃЌ
ЃЌ![]() ЃЌЁрES=
ЃЌЁрES=![]() ЃЌ
ЃЌ
Жј![]() =
=![]()
![]()
Ёп![]() ,Ёр
,Ёр![]()
![]()
![]() ЃЌ
ЃЌ![]() ЃЈ
ЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
злЩЯЫљЪіЃЌЗћКЯЬѕМўЕФЕуFЕФзјБъЪЧ(![]() ,-2)ЃЌЃЈ
,-2)ЃЌЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ.
ЃЉ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
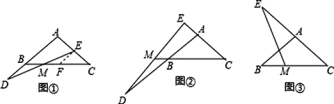
ЁОЬтФПЁПвбжЊЃЌдкЁїABCжаЃЌAB=ACЃЌдкЩфЯпABЩЯНиШЁЯпЖЮBDЃЌдкЩфЯпCAЩЯНиШЁЯпЖЮCEЃЌСЌНсDEЃЌDEЫљдкжБЯпНЛжБЯпBCгкЕуMЃЎ
ВТЯыЃКЕБЕуDдкБпABЕФбгГЄЯпЩЯЃЌЕуEдкБпACЩЯЪБЃЌЙ§ЕуEзїEFЁЮABНЛBCгкЕуFЃЌШчЭМЂйЃЎШєBD=CEЃЌдђЯпЖЮDMЁЂEMЕФДѓаЁЙиЯЕЮЊ ЃЎ
ЬНОПЃКЕБЕуDдкБпABЕФбгГЄЯпЩЯЃЌЕуEдкБпCAЕФбгГЄЯпЩЯЪБЃЌШчЭМЂкЃЎШєBD=CEЃЌХаЖЯЯпЖЮDMЁЂEMЕФДѓаЁЙиЯЕЃЌВЂМгвджЄУїЃЎ
ЭиеЙЃКЕБЕуDдкБпABЩЯЃЈЕуDВЛгыAЁЂBжиКЯЃЉЃЌЕуEдкБпCAЕФбгГЄЯпЩЯЪБЃЌШчЭМЂлЃЎШєBD=1ЃЌCE=4ЃЌDM=0.7ЃЌЧѓEMЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгаЦпеХе§УцЗжБ№БъгаЪ§зжЉ3ЃЌЉ2ЃЌЉ1ЃЌ0ЃЌ1ЃЌ2ЃЌ3ЕФПЈЦЌЃЌЫќУЧГ§Ъ§зжВЛЭЌЭтЦфгрШЋВПЯрЭЌЃЎЯжНЋЫќУЧБГУцГЏЩЯЃЌЯДдШКѓДгжаЫцЛњГщШЁвЛеХЃЌМЧПЈЦЌЩЯЕФЪ§зжЮЊaЃЌдђЪЙЙигкxЕФвЛдЊЖўДЮЗНГЬx2Љ2ЃЈaЉ1ЃЉx+aЃЈaЉ3ЃЉЃН0гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЌЧввдxЮЊздБфСПЕФЖўДЮКЏЪ§yЃНx2ЉЃЈa2+1ЃЉxЉa+2ЕФЭМЯѓВЛОЙ§ЕуЃЈ1ЃЌ0ЃЉЕФИХТЪЪЧЃЈЁЁЁЁЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕуPДг![]() ГіЗЂЃЌбиЫљЪОЗНЯђдЫЖЏЃЌУПЕБХіЕНГЄЗНаЮOABCЕФБпЪБЛсНјааЗДЕЏЃЌЗДЕЏЪБЗДЩфНЧЕШгкШыЩфНЧЃЌЕБЕуPЕк2018ДЮХіЕНГЄЗНаЮЕФБпЪБЃЌЕуPЕФзјБъЮЊ______ЃЎ
ГіЗЂЃЌбиЫљЪОЗНЯђдЫЖЏЃЌУПЕБХіЕНГЄЗНаЮOABCЕФБпЪБЛсНјааЗДЕЏЃЌЗДЕЏЪБЗДЩфНЧЕШгкШыЩфНЧЃЌЕБЕуPЕк2018ДЮХіЕНГЄЗНаЮЕФБпЪБЃЌЕуPЕФзјБъЮЊ______ЃЎ

ЁОД№АИЁП![]()
ЁОНтЮіЁП
ИљОнЗДЩфНЧгыШыЩфНЧЕФЖЈвхзїГіЭМаЮЃЛгЩЭМПЩжЊЃЌУП6ДЮЗДЕЏЮЊвЛИібЛЗзщвРДЮбЛЗЃЌгУ2018Г§вд6ЃЌИљОнЩЬКЭгрЪ§ЕФЧщПіШЗЖЈЫљЖдгІЕФЕуЕФзјБъМДПЩЃЎ
НтЃКШчЭМЫљЪОЃКОЙ§6ДЮЗДЕЏКѓЖЏЕуЛиЕНГіЗЂЕу![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЕБЕуPЕк2018ДЮХіЕНОиаЮЕФБпЪБЮЊЕк337ИібЛЗзщЕФЕк2ДЮЗДЕЏЃЌ
ЕБЕуPЕк2018ДЮХіЕНОиаЮЕФБпЪБЮЊЕк337ИібЛЗзщЕФЕк2ДЮЗДЕЏЃЌ
![]() ЕуPЕФзјБъЮЊ
ЕуPЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() ЃЎ
ЃЎ
ЁОЕуОІЁП
ДЫЬтжївЊПМВщСЫЕуЕФзјБъЕФЙцТЩЃЌзїГіЭМаЮЃЌЙлВьГіУП6ДЮЗДЕЏЮЊвЛИібЛЗзщвРДЮбЛЗЪЧНтЬтЕФЙиМќЃЎ
ЁОЬтаЭЁПЬюПеЬт
ЁОНсЪјЁП
15
ЁОЬтФПЁПЮЊСЫБЃЛЄЛЗОГЃЌФГЙЋНЛЙЋЫООіЖЈЙКТђAЁЂBСНжжаЭКХЕФШЋаТЛьКЯЖЏСІЙЋНЛГЕЙВ10СОЃЌЦфжаAжжаЭКХУПСОМлИёЮЊaЭђдЊЃЌУПФъНкЪЁгЭСПЮЊ![]() ЭђЩ§ЃЛBжжаЭКХУПСОМлИёЮЊbЭђдЊЃЌУПФъНкЪЁгЭСПЮЊ
ЭђЩ§ЃЛBжжаЭКХУПСОМлИёЮЊbЭђдЊЃЌУПФъНкЪЁгЭСПЮЊ![]() ЭђЩ§ЃКОЕїВщЃЌЙКТђвЛСОAаЭГЕБШЙКТђвЛСОBаЭГЕЖр20ЭђдЊЃЌЙКТђ2СОAаЭГЕБШЙКТђ3СОBаЭГЕЩй60ЭђдЊЃЎ
ЭђЩ§ЃКОЕїВщЃЌЙКТђвЛСОAаЭГЕБШЙКТђвЛСОBаЭГЕЖр20ЭђдЊЃЌЙКТђ2СОAаЭГЕБШЙКТђ3СОBаЭГЕЩй60ЭђдЊЃЎ
![]() ЧыЧѓГіaКЭbЃЛ
ЧыЧѓГіaКЭbЃЛ
![]() ШєЙКТђетХњЛьКЯЖЏСІЙЋНЛГЕУПФъФмНкЪЁ
ШєЙКТђетХњЛьКЯЖЏСІЙЋНЛГЕУПФъФмНкЪЁ![]() ЭђЩ§ЦћгЭЃЌЧѓЙКТђетХњЛьКЯЖЏСІЙЋНЛГЕашвЊЖрЩйЭђдЊЃП
ЭђЩ§ЦћгЭЃЌЧѓЙКТђетХњЛьКЯЖЏСІЙЋНЛГЕашвЊЖрЩйЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§y1ЃНkx+bЃЈkЁй0ЃЉгыЗДБШР§КЏЪ§![]() ЃЈnЁй0ЃЉНЛгкAЁЂBСНЕуЃЌЙ§AзїACЁЭxжсгкЕуCЃЌOCЃН3ЃЌcosЁЯAOCЃН
ЃЈnЁй0ЃЉНЛгкAЁЂBСНЕуЃЌЙ§AзїACЁЭxжсгкЕуCЃЌOCЃН3ЃЌcosЁЯAOCЃН![]() ЃЌЕуBЕФзјБъЪЧЃЈmЃЌЉ2ЃЉЃЎ
ЃЌЕуBЕФзјБъЪЧЃЈmЃЌЉ2ЃЉЃЎ
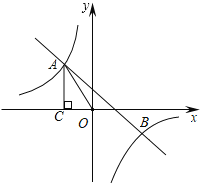
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉНсКЯЭМЯѓЃЌЕБy1ЃМy2ЪБЃЌжБНгаДГіздБфСПЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГМЭФюЦЗзЈТєЕъЩЯжмХњЗЂТђНј100МўAМЭФюЦЗКЭ300МўBМЭФюЦЗЃЌЛЈЗб9600дЊЃЛБОжмХњЗЂТђНј200МўAМЭФюЦЗКЭ100МўBМЭФюЦЗЃЌЛЈЗб6200дЊЃЎ
ЃЈ1ЃЉЧѓУПМўAМЭФюЦЗКЭBМЭФюЦЗЕФХњЗЂМлИїЮЊЖрЩйдЊЃП
ЃЈ2ЃЉОЪаГЁЕїбаЃЌЕБAМЭФюЦЗУПМўЕФЯњЪлМлЮЊ30дЊЪБЃЌУПжмПЩЯњЪл200МўЃЛЕБУПМўЕФЯњЪлМлУПдіМг1дЊЃЌУПжмЕФЯњЪлЪ§СПНЋМѕЩй10МўЃЎЕБУПМўЕФЯњЪлМлaЮЊЖрЩйЪБЃЌИУМЭЬЌЦЗзЈТєЕъЯњЪлAМЭФюЦЗУПжмЛёЕУЕФРћШѓWзюДѓЃПВЂЧѓГізюДѓРћШѓЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
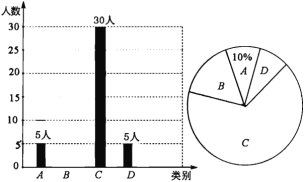
ЁОЬтФПЁПбыЪгЁАОЕфгНСїДЋЁБПЊВЅвдРДЪмЕНЩчЛсЙуЗКЙизЂ.ЮвЪаФГаЃОЭЁАжаЛЊЮФЛЏЮвДЋГаЁЊЁЊЕиЗНЯЗЧњНјаЃдАЁБЕФЯВАЎЧщПіНјааСЫЫцЛњЕїВщЃЌЖдЪеМЏЕФаХЯЂНјааЭГМЦЃЌЛцжЦСЫЯТУцСНИБЩаВЛЭъећЕФЭГМЦЭМ.ЧыФуИљОнЭГМЦЭМЫљЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЭМжаAБэЪОЁАКмЯВЛЖЁБЃЌBБэЪОЁАЯВЛЖЁБЃЌCБэЪОЁАвЛАуЁБЃЌDБэЪОЁАВЛЯВЛЖЁБ.
ЃЈ1ЃЉБЛЕїВщЕФзмШЫЪ§ЪЧ_____________ШЫЃЌЩШаЮЭГМЦЭМжаCВПЗжЫљЖдгІЕФЩШаЮдВаФНЧЕФЖШЪ§ЮЊ_______.
ЃЈ2ЃЉВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ3ЃЉШєИУаЃЙВгабЇЩњ1800ШЫЃЌЧыИљОнЩЯЪіЕїВщНсЙћЃЌЙРМЦИУаЃбЇЩњжаAРрга__________ШЫЃЛ
ЃЈ4ЃЉдкГщШЁЕФAРр5ШЫжаЃЌИеКУга3ИіХЎЩњ2ИіФаЩњЃЌДгжаЫцЛњГщШЁСНИіЭЌбЇЕЃШЮСННЧЩЋЃЌгУЪїаЮЭМЛђСаБэЗЈЧѓГіБЛГщЕНЕФСНИібЇЩњадБ№ЯрЭЌЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЕШБпШ§НЧаЮЕФЖЅЕуAЃЈ1ЃЌ1ЃЉЃЌBЃЈ3ЃЌ1ЃЉЃЌЙцЖЈАбЕШБпЁїABCЁАЯШбиxжсЗелЃЌдйЯђзѓЦНвЦ1ИіЕЅЮЛЁБЮЊвЛДЮБфЛЛЃЌCЕуЕФЖдгІЕуМЧЮЊC1ЃЎШчЙћетбљСЌајОЙ§2019ДЮБфЛЛКѓЃЌдђC2019ЕФзјБъЮЊЃЈЁЁЁЁЃЉ
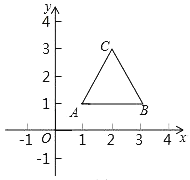
A. ЃЈЉ2017ЃЌЉ1Љ![]() ЃЉB. ЃЈЉ2017ЃЌ1+
ЃЉB. ЃЈЉ2017ЃЌ1+![]() ЃЉ
ЃЉ
C. ЃЈЉ2018ЃЌЉ1Љ![]() ЃЉD. ЃЈЉ2018ЃЌ1+
ЃЉD. ЃЈЉ2018ЃЌ1+![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com