
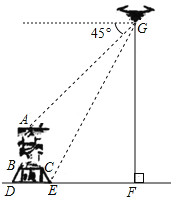
【题目】为了测量重庆有名的观景点南山大金鹰的大致高度,小南同学使用的无人机进行观察,当无人机与大金鹰侧面在同一平面,且距离水平面垂直高度GF为100米时,小南调整摄像头方向,当俯角为45°时,恰好可以拍摄到金鹰的头顶A点;当俯角为63°时,恰好可以拍摄到金鹰底座点E.已知大金鹰是雄踞在一人造石台上,石台侧面CE长12.5米,坡度为1:0.75,石台上方BC长10米,头部A点位于BC中点正上方.则金鹰自身高度约( )米.(结果保留一位小数,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
作AM⊥DF于M,AHGF于H,则AM=HF,AH=MF,在Rt△EFG中,由三角函数求出EF=![]() ≈51.02,由石台侧面CE坡度为1:0.75,求出石台侧面CE宽度为12.5×
≈51.02,由石台侧面CE坡度为1:0.75,求出石台侧面CE宽度为12.5×![]() =7.5,高度为10,求出ME=
=7.5,高度为10,求出ME=![]() BC=12.5,得出AH=MF=63.52,证出△AGH是等腰直角三角形,得出GH=AH=63.52,求出AM=HF=100-63.52≈36.5(米),即可得出答案.
BC=12.5,得出AH=MF=63.52,证出△AGH是等腰直角三角形,得出GH=AH=63.52,求出AM=HF=100-63.52≈36.5(米),即可得出答案.
解:作AM⊥DF于M,AH⊥GF于H,如图所示:
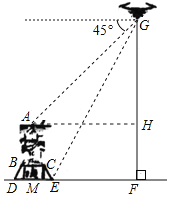
则AM=HF,AH=MF,
在Rt△EFG中,∠GEF=63°,
∵tan∠GEF=![]() ,∴EF=
,∴EF=![]() ≈
≈![]() =51.02,
=51.02,
∵石台侧面CE长12.5米,坡度为1:0.75,
∴石台侧面CE宽度为12.5×![]() =7.5,高度为12.5×
=7.5,高度为12.5×![]() =10,
=10,
∵石台上方BC长10米,头部A点位于BC中点正上方,
∴ME=![]() BC+7.5=5+7.5=12.5,
BC+7.5=5+7.5=12.5,
∴AH=MF=12.5+51.02=63.52,
在Rt△AGH中,∠AGH=90°-45°=45°,
∴△AGH是等腰直角三角形,
∴GH=AH=63.52,
∴AM=HF=100-63.52≈36.5(米),
∴金鹰自身高度约为36.5-10=26.5(米);
故选:A.


科目:初中数学 来源: 题型:
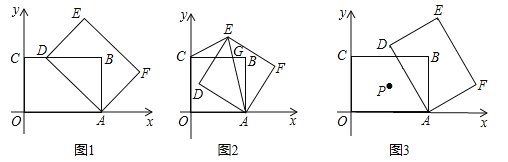
【题目】矩形![]() ,
,![]() ,
,![]() ,
,![]() ,(
,(![]() ),以
),以![]() 为旋转中心顺时针旋转矩形
为旋转中心顺时针旋转矩形![]() ,得到矩形
,得到矩形![]() .
.
(1)如图1,当点![]() 落在边
落在边![]() 上时,求
上时,求![]() 的长;
的长;
(2)如图2,当![]() 时,矩形
时,矩形![]() 的对角线
的对角线![]() 交矩形
交矩形![]() 的边
的边![]() 于点
于点![]() ,连结
,连结![]() ,若
,若![]() 是等腰三角形,求直线
是等腰三角形,求直线![]() 的解析式.
的解析式.
(3)如图3,当![]() 时,矩形
时,矩形![]() 的对称中心为点
的对称中心为点![]() .
.![]() 的面积为
的面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解同学们对网络游戏的喜好和作业量多少的相关性,小明随机对年级50名同学进行了调查,并将调查的情况进行了整理,如下表:
作业量多少 网络游戏的喜好 | 认为作业多 | 认为作业不多 | 合计 |
喜欢网络游戏 | 18 | 9 | 27 |
不喜欢网络游戏 | 8 | 15 | 23 |
合计 | 26 | 24 | 50 |
如果小明再随机采访一名同学,那么这名同学是“喜欢网络游戏并认为作业多”的可能性______“不喜欢网络游戏并认为作业不多”的可能性.(填“>”,“=”或“<”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解高二年级男生定点投篮的情况,随机选取该校高二年级部分男生进行测试,每人投篮五次,以下是根据每人投中次數绘制的统计图的一部分,
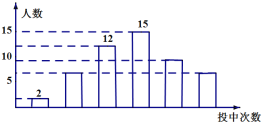
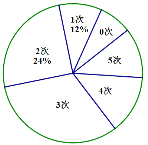
根据以上信息解答下列问题:
(1)被调查的男生中,投中次数为2次的有_____人,投中次数为1次的男生人数占被调查男生总数的百分比为_____%;
(2)被调查男生的总数为_____人,扇形统计图中投中次数为3次的圆心角的度数为_____;
(3)若该校高二年级男生有200人,根据调查结果,估计该年级男生投中次数不少于3次的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,Rt△ABC中,∠ACB=90°,AC=5,BC=12,点D在边AB上,以AD为直径的⊙O,与边BC有公共点E,则AD的最小值是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近一周,各个学校均在紧张有序地进行中考模拟考试,学生们通过模拟考试来调整自己的状态并了解自己的学业水平.某中学物理教研组想通过此次中考模拟的成绩来预估中考的各个分数段人数,在全年级随机抽取了男.女各40名学生的成绩(满分为80分,女生成绩中最低分为45分),并将数据进行整理分析,给出了下面部分信息:
①男生成绩扇形统计图和女生成绩频数分布直方图如下:(数据分组为A组:x<50;B组:50≤x<60;C组:60≤x<70;D组:70≤x≤80)

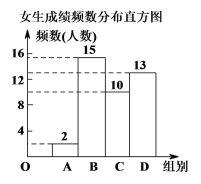
②男生C组中全部15名学生的成绩为:
63,69,64,62,68,69,65,69,65,66,67,61,67,66,69.
③两组数据的平均数.中位数.众数.满分率.极差(单位:分)如下表所示:
平均数 | 中位数 | 众数 | 满分率 | 极差 | |
男生 | 70 | b | c | 25% | 32 |
女生 | 70 | 68 | 78 | 15% | d |
(1)扇形统计图A组学生中所对应的圆心角α的度数为 ,中位数b= ,众数c= ,极差d= .
(2)通过以上的数据分析,你认为 (填“男生”或“女生”)的物理成绩更好,并说明理由:
① ;② .
(3)若成绩在70分(包含70分)以上为优秀,请你估计该校1200名学生中此次考试中优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把三角形按如图所示的规律拼图案,其中第①个图案中有4个三角形,第②个图案中有6个三角形,第③个图案中有8个三角形,…,按此规律排列下去,则第⑦个图案中三角形的个数为( )
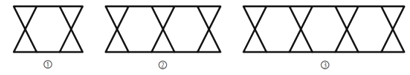
A. 12 B. 14 C. 16 D. 18
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条射线BA//CD,PB和PC分别平分∠ABC和∠DCB,AD过点P,分别交AB,CD与点A,D.
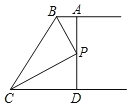
(1)求∠BPC的度数;
(2)若![]() ,求AB+CD的值;
,求AB+CD的值;
(3)若![]() 为a,
为a,![]() 为b,
为b,![]() 为c,求证:a+b=c.
为c,求证:a+b=c.
查看答案和解析>>
科目:初中数学 来源: 题型:
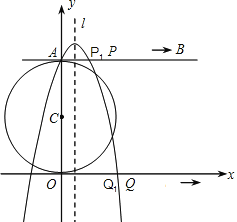
【题目】如图,在平面直角坐标系中,以点C(0,4)为圆心,半径为4的圆交y轴正半轴于点A,AB是⊙C的切线.动点P从点A开始沿AB方向以每秒1个单位长度的速度运动,点Q从O点开始沿x轴正方向以每秒4个单位长度的速度运动,且动点P、Q从点A和点O同时出发,设运动时间为t(秒).
(1)当t=1时,得到P1、Q1,求经过A、P1、Q1三点的抛物线解析式及对称轴l;
(2)当t为何值时,直线PQ与⊙C相切?并写出此时点P和点Q的坐标;
(3)在(2)的条件下,抛物线对称轴l上存在一点N,使NP+NQ最小,求出点N的坐标并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com