Question

【题目】如图，在等边△ABC中，点D，E分别在边BC，AB上，且BD=AE，AD与CE交于点F，作CM⊥AD，垂足为M，下列结论不正确的是（ ）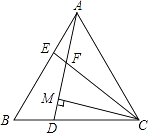

A.AD=CE
B.MF= CF
C.∠BEC=∠CDA
D.AM=CM

Answer 1

【答案】D
【解析】解：A正确；理由如下：
∵△ABC是等边三角形，
∴∠BAC=∠B=60°，AB=AC
又∵AE=BD
在△AEC与△BDA中，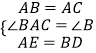
，
∴△AEC≌△BDA（SAS），
∴AD=CE；
B正确；理由如下：
∵△AEC≌△BDA，
∴∠BAD=∠ACE，
∴∠AFE=∠ACE+∠CAD=∠BAD+∠CAD=∠BAC=60°，
∴∠CFM=∠AFE=60°，
∵CM⊥AD，
∴在Rt△CFM中，∠FCM=30°，
∴MF= CF；
C正确；理由如下：
∵∠BEC=∠BAD+∠AFE，∠AFE=60°，
∴∠BEC=∠BAD+∠AFE=∠BAD+60°，
∵∠CDA=∠BAD+∠CBA=∠BAD+60°，
∴∠BEC=∠CDA；
D不正确；理由如下：
要使AM=CM，则必须使∠DAC=45°，由已知条件知∠DAC的度数为大于0°小于60°均可，
∴AM=CM不成立；
故选：D．
【考点精析】本题主要考查了等边三角形的性质和含30度角的直角三角形的相关知识点，需要掌握等边三角形的三个角都相等并且每个角都是60°；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半才能正确解答此题．