
Ζ÷Έω Θ®1Θ©“άΧβ“βΘ§ΒΟΘΚΓςAFGΓΔΓςBEGΈΣΒ»±Ώ»ΐΫ«–ΈΘ§Υυ“‘”–FG=AG=xΘ§EG=BG=2$\sqrt{3}$-xΘ§ΓœEGF=60ΓψΘ§”…»ΐΫ«–ΈΒΡΟφΜΐΕ®άμΦ¥Ω…ΒΟΒΫy”κxΒΡΚ· ΐΙΊœΒ ΫΘΜ
Θ®2Θ©”…Θ®1Θ©÷ΣΓœEGF=60ΓψΘ§–ηΖ÷άύΧ÷¬έΘΚΓœEFG=90ΓψΘ§ΓœFEG=90ΓψΘ§ΝΫ÷÷«ιΩωΘ§”…Κ§30ΓψΒΡ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Φ¥Ω…«σ≥ωΫα¬έΘΜ
Θ®3Θ©»τΥΡ±Ώ–ΈGFEBΙΙ≥…ΤΫ––ΥΡ±Ώ–Έ ±Θ§“Ή÷ΛΓςAFGΘ§ΓςBEGΘ§ΓςCEFΘ§ΓςEFG «»ΪΒ»ΒΡΒ»±Ώ»ΐΫ«–ΈΘ§“Ή«σSΓςGEFΘ°
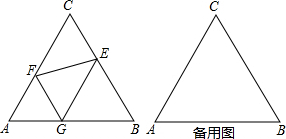
Ϋβ¥π  ΫβΘΚΘ®1Θ©ΓΏΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§GFΓΈBCΘ§
ΫβΘΚΘ®1Θ©ΓΏΓςABC «Β»±Ώ»ΐΫ«–ΈΘ§GFΓΈBCΘ§
ΓύΓœAGF=ΓœB=60ΓψΘ§
ΓύΓςAFG «Β»±Ώ»ΐΫ«–ΈΘ§
Ά§άμΓςBEGΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύFG=AG=xΘ§EG=BG=2$\sqrt{3}$-xΘ§ΓœEGF=60ΓψΘ§
y=$\frac{1}{2}xΘ®2\sqrt{3}-xΘ©sin60Γψ$=-$\frac{\sqrt{3}}{4}{x}^{2}+\frac{3}{2}x$Θ§Ε®“ε”ρΘΚΘ®0Θ§2$\sqrt{3}$Θ©ΘΜ
Θ®2Θ©»τΓœEFG=90ΓψΘ§”÷ΓœEGF=60ΓψΘ§Υυ“‘Θ§”–x=$\frac{1}{2}$Θ®2$\sqrt{3}$-xΘ©Θ§ΫβΒΟΘΚx=$\frac{2\sqrt{3}}{3}$Θ§
»τΓœFEG=90ΓψΘ§‘ρ$\frac{1}{2}x=2\sqrt{3}-x$Θ§ΫβΒΟΘΚx=$\frac{4\sqrt{3}}{3}$Θ§
Υυ“‘Θ§Ρή ΙΓςGEF≥…ΈΣ÷±Ϋ«»ΐΫ«–ΈΘ§AGΒΡ≥ΛΈΣ$\frac{2\sqrt{3}}{3}$Μρ$\frac{4\sqrt{3}}{3}$ΘΜ
Θ®3Θ©»τΥΡ±Ώ–ΈGFEBΙΙ≥…ΤΫ––ΥΡ±Ώ–Έ ±Θ§
”…Θ®1Θ©ΓςAFGΚΆΓςBEGΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύΓςCEG «Β»±Ώ»ΐΫ«–ΈΘ§
ΓύΓœEFG=ΓœFEG=60ΓψΘ§
ΓύΓςEFGΈΣΒ»±Ώ»ΐΫ«–ΈΘ§
ΓύEF=FG=AG=GB=$\frac{1}{2}AB$=$\sqrt{3}$Θ§
ΓύSAGEF=$\frac{1}{2}FG•EGsin60Γψ$=$\frac{1}{2}ΓΝ\sqrt{3}ΓΝ\sqrt{3}ΓΝ\frac{\sqrt{3}}{2}$=$\frac{3\sqrt{3}}{4}$Θ°
ΒψΤά ±ΨΧβ÷ς“ΣΩΦ≤ιΝΥΒ»±Ώ»ΐΫ«–ΈΒΡ≈–Ε®ΚΆ–‘÷ Θ§»ΐΫ«–ΈΒΡΟφΜΐΕ®άμΘ§ΤΫ––ΥΡ±Ώ–ΈΒΡ–‘÷ Θ§Κ§30ΓψΒΡ÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Θ§ΡήΝιΜν”Π”Ο’β–©–‘÷ «ΫβΧβΒΡΙΊΦϋΘ§Ά§ ±ΉΔ“βΖ÷άύΥΦœκΒΡ”Π”ΟΘ°


 –Γ―ß―ßœΑΚΟΑο ÷œΒΝ–¥πΑΗ
–Γ―ß―ßœΑΚΟΑο ÷œΒΝ–¥πΑΗ –Γ―ßΆ§≤Ϋ»ΐΝΖΚΥ–ΡΟήΨμœΒΝ–¥πΑΗ
–Γ―ßΆ§≤Ϋ»ΐΝΖΚΥ–ΡΟήΨμœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 0 | BΘ° | -2 | CΘ° | Π– | DΘ° | -1 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
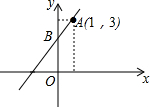 »γΆΦΘ§÷±œΏy=kx+bΨ≠ΙΐAΘ®1Θ§3Θ©ΚΆBΘ®0Θ§2Θ©Θ§‘ρΙΊ”ΎxΒΡ≤ΜΒ» Ϋkx+bΘΦ3ΒΡΫβΦ· «Θ®ΓΓΓΓΘ©
»γΆΦΘ§÷±œΏy=kx+bΨ≠ΙΐAΘ®1Θ§3Θ©ΚΆBΘ®0Θ§2Θ©Θ§‘ρΙΊ”ΎxΒΡ≤ΜΒ» Ϋkx+bΘΦ3ΒΡΫβΦ· «Θ®ΓΓΓΓΘ©| AΘ° | xΘΦ1 | BΘ° | xΘΨ1 | CΘ° | xΘΦ0 | DΘ° | xΘΨ0 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
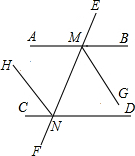 »γΆΦΘ§“―÷ΣABΓΈCDΘ§MGΓΔNHΖ÷±πΤΫΖ÷ΓœBMN”κΓœCNMΘ§ ‘ΥΒΟςNHΓΈMGΘ°
»γΆΦΘ§“―÷ΣABΓΈCDΘ§MGΓΔNHΖ÷±πΤΫΖ÷ΓœBMN”κΓœCNMΘ§ ‘ΥΒΟςNHΓΈMGΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
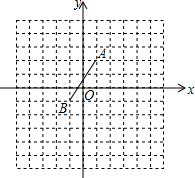 »γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣΝΫΒψAΘ®1Θ§2Θ©Θ§BΘ®-1Θ§-1Θ©Θ§
»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§“―÷ΣΝΫΒψAΘ®1Θ§2Θ©Θ§BΘ®-1Θ§-1Θ©Θ§≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
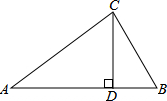 »γΆΦΘ§CD «RtΓςABC–±±ΏAB…œΒΡΗΏΘ§CD=6Θ§BD=4Θ§‘ρABΒΡ≥ΛΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§CD «RtΓςABC–±±ΏAB…œΒΡΗΏΘ§CD=6Θ§BD=4Θ§‘ρABΒΡ≥ΛΈΣΘ®ΓΓΓΓΘ©| AΘ° | 10 | BΘ° | 11 | CΘ° | 12 | DΘ° | 13 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
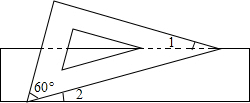 »γΆΦΘ§”–“ΜΩιΚ§”–60ΓψΫ«ΒΡ÷±Ϋ«»ΐΫ«ΑεΒΡΝΫΗωΕΞΒψΖ≈‘Ύ≥ΛΖΫ–ΈΒΡΕ‘±Ώ…œΘ°»γΙϊΓœ1=16ΓψΘ§Ρ«Ο¥Γœ2ΒΡΕ» ΐ «14ΓψΘ°
»γΆΦΘ§”–“ΜΩιΚ§”–60ΓψΫ«ΒΡ÷±Ϋ«»ΐΫ«ΑεΒΡΝΫΗωΕΞΒψΖ≈‘Ύ≥ΛΖΫ–ΈΒΡΕ‘±Ώ…œΘ°»γΙϊΓœ1=16ΓψΘ§Ρ«Ο¥Γœ2ΒΡΕ» ΐ «14ΓψΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
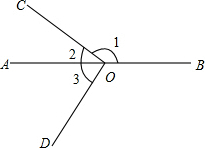 »γΆΦΘ§“―÷ΣΒψO‘Ύ÷±œΏAB…œΘ§COΓΆDOΘ§»τΓœ1=155ΓψΘ§‘ρΓœ3ΒΡΕ» ΐΈΣΘ®ΓΓΓΓΘ©
»γΆΦΘ§“―÷ΣΒψO‘Ύ÷±œΏAB…œΘ§COΓΆDOΘ§»τΓœ1=155ΓψΘ§‘ρΓœ3ΒΡΕ» ΐΈΣΘ®ΓΓΓΓΘ©| AΘ° | 35Γψ | BΘ° | 45Γψ | CΘ° | 55Γψ | DΘ° | 65Γψ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
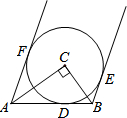 »γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§“‘ΒψCΈΣ‘≤–ΡΉςΓ―CΘ§”κAB«–”ΎΒψDΘ§ΙΐΒψAΓΔBΖ÷±πΉςΓ―CΒΡ«–œΏAFΓΔBEΘ§«–ΒψΈΣFΓΔEΒψΘ°«σ÷ΛΘΚAFΓΈBEΘ°
»γΆΦΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§“‘ΒψCΈΣ‘≤–ΡΉςΓ―CΘ§”κAB«–”ΎΒψDΘ§ΙΐΒψAΓΔBΖ÷±πΉςΓ―CΒΡ«–œΏAFΓΔBEΘ§«–ΒψΈΣFΓΔEΒψΘ°«σ÷ΛΘΚAFΓΈBEΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com