
在平面直角坐标系xOy中,已知二次函数的图像经过原点及点A(1,2),与x轴相交于另一点B(3,0),将点B向右平移3个单位得点C.
(1)求二次函数的解析式;
(2)点M在线段OC上,平面内有一点Q,使得四边形ABMQ为菱形,求点M坐标;
(3)点P在线段OC上,从O点出发向C点运动,过P点作x轴的垂线,交直线AO于D点,以PD为边在PD的右侧作正方形PDEF(当P点运动时,点D、点E、点F也随之运动);
①当点E在二次函数的图像上时,求OP的长;
②若点P从O点出发向C点做匀速运动,速度为每秒1个单位长度,若P点运动t秒时,直线AC与以DE为直径的⊙M相切,直接写出此刻t的值.

(1)y=-x2+3x;(2)(1,0)或(3-2 ,0)或(3+2
,0)或(3+2 ,0);(3)
,0);(3) 或
或 .
.
【解析】
试题分析:(1)可设二次函数的解析式为y=ax2+bx+c,利用二次函数的图象经过原点及点A(1,2),B(3,0),分别代入求出a,b,c的值即可;
(2)分M是AB的垂直平分线与x轴的交点;M在B点左边并且BM=AB;M在B点右边并且BM=AB;三种情况讨论可得点M坐标;
(3)①过A点作AH⊥x轴于H点,根据DP∥AH,得出△OPD∽△OHA,进而求出OP的长;
②分两种情况讨论,求出t的值即可.
试题解析:(1)设二次函数的解析式为y=ax2+bx+c,
∵二次函数的图象经过原点及点A(1,2),B(3,0),
∴ ,
,
解得 .
.
故二次函数解析式为:y=-x2+3x;
(2)M是AB的垂直平分线与x轴的交点,点M坐标是(1,0);
M在B点左边并且BM=AB,点M坐标是(3-2 ,0);
,0);
M在B点右边并且BM=AB,点M坐标是(3+2 ,0);
,0);
故点M坐标为(1,0)或(3-2 ,0)或(3+2
,0)或(3+2 ,0);
,0);
(3)①由已知可得C(6,0)
如图:过A点作AH⊥x轴于H点,
∵DP∥AH,
∴△OPD∽△OHA,
∴ ,
,
即 ,
,
∴PD=2a,
∵正方形PDEF,
∴E(3a,2a),
∵E(3a,2a)在二次函数y1=-x2+3x的图象上,
∴a= ;
;
即OP= .
.
②直线AC与以DE为直径的⊙M相切,此刻t的值为: 或
或 .
.
考点:二次函数综合题.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源:2013-2014学年江苏省张家港市九年级5月网上阅卷适应性考试数学试卷(解析版) 题型:选择题
如图,在梯形ABCD中,AD∥BC,∠B=50°,∠C=80°,AE∥CD交BC于点E,若AD=2,BC=5,则边CD的长是

A. B.
B. C.3 D.4
C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省常州市九年级中考一模数学试卷(解析版) 题型:选择题
若一次函数 ,当
,当 的值减小1,
的值减小1, 的值就减小2,则当
的值就减小2,则当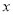 的值增加2时,
的值增加2时, 的值( )
的值( )
A.增加4 B.减小4 C.增加2 D.减小2
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省宜兴市和桥学区九年级下学期期中考试(一模)数学试卷(解析版) 题型:解答题
有5张形状、大小和质地都相同的卡片,正面分别写有字母:A,B,C,D,E和一个等式,背面完全一致.现将5张卡片分成两堆,第一堆:A,B,C;第二堆:D,E,并从第一堆中抽出第一张卡片,再从第二堆中抽出第二张卡片,背面向上洗匀.

(1)请用画树形图或列表法表示出所有可能结果;(卡片可用A,B,C,D,E表示)
(2)将“第一张卡片上x的值是第二张卡片中方程的解”记作事件M,求事件M的概率.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省宜兴市和桥学区九年级下学期期中考试(一模)数学试卷(解析版) 题型:填空题
如图,△ABC中,∠A=90°,∠C=75°,AC=6,DE垂直平分BC,则BE= .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省九年级新课结束考试数学试卷(解析版) 题型:解答题
如图①,一条笔直的公路上有A、B、C三地,B、C两地相距150千米,甲、乙两辆汽车分别从B、C两地同时出发,沿公路匀速相向而行,分别驶往C、B两地.甲、乙两车到A地的距离y1、y2(千米)与行驶时间x(时)的关系如图②所示.根据图象进行以下探究:


(1)请在图①中标出A地的位置,并作简要的文字说明;
(2)求图②中M点的坐标,并解释该点的实际意义;
(3)在图②中补全甲车的函数图象,求甲车到A地的距离y1与行驶时间x的函数关系式;
(4)A地设有指挥中心,指挥中心及两车都配有对讲机,两部对讲机在15千米之内(含15千米)时能够互相通话,求两车可以同时与指挥中心用对讲机通话的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com