
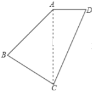
【题目】如图,在四边形ABCD中,AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,则∠DAB的度数是______°.
【答案】135°
【解析】
由已知可得AB=BC,从而可求得∠BAC的度数.设AB=2x ,通过计算证明AC2+AD2=CD2,从而证得ΔACD是直角三角形,即可得到∠DAC=90°,从而求得∠DAB的度数.
解:∵AB:BC:CD:DA=2:2:3:1,且∠ABC=90°,
∴AB=BC,
∴∠BAC=∠ACB=45°,
∴设AB=2x,则BC=2x,CD=3x,DA=x,
∴AC2=AB2+BC2=(2x)2+(2x)2=8x2
又CD2-AD2=(3x)2-x2=8x2
∴AC2= CD2-AD2
∵AC2+AD2=CD2
∴ΔACD是直角三角形,
∴∠DAC=90°,
∴∠DAB=45°+90°=135°.
故答案是:135°.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为1,点A与原点重合,点B在y轴的正半轴上,点D在x轴的负半轴上,将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置,B'C′与CD相交于点M,则点M的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
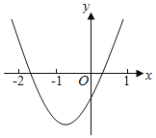
【题目】已知二次函数y=ax2+bx+c(a≠0)图象如图所示,下列结论:①abc<0;②2a﹣b<0;③b2>(a+c)2;④点(﹣3,y1),(1,y2)都在抛物线上,则有y1>y2.其中正确的结论有( )
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
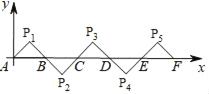
【题目】如图所示,在平面直角坐标系中A(0,0),B(2,0),△AP1B是等腰直角三角形,且∠P1=90°,把△AP1B绕点B顺时针旋转180°,得到△BP2C;把△BP2C绕点C顺时针旋转180°,得到△CP3D,依此类推,则旋转第2017次后,得到的等腰直角三角形的直角顶点P2018的坐标为( )
A. (4030,1) B. (4029,﹣1)
C. (4033,1) D. (4035,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
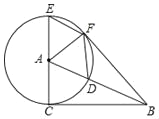
【题目】在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF、BF、DF
(1)求证:BF是⊙A的切线.
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王明同学随机抽查某市![]() 个小区所得到的绿化率情况,结果如下表:
个小区所得到的绿化率情况,结果如下表:
小区绿化率 |
|
|
|
|
小区个数 |
|
|
|
|
则关于这![]() 个小区的绿化率情况,下列说法错误的是( )
个小区的绿化率情况,下列说法错误的是( )
A. 极差是13% B. 众数是25% C. 中位数是25% D. 平均数是26.2%
查看答案和解析>>
科目:初中数学 来源: 题型:
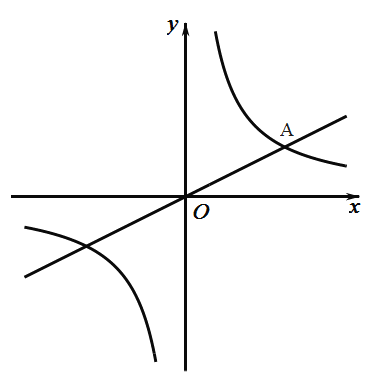
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 在第一象限交于
在第一象限交于![]() 点,且点
点,且点![]() 的横坐标为4,点
的横坐标为4,点![]() 在双曲线上.
在双曲线上.
(1)求双曲线的函数解析式;
(2)若点![]() 的纵坐标为8,试判断
的纵坐标为8,试判断![]() 形状,并说明理由.
形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店将进价为8元的商品按每件10元售出,每天可售出200件,现在采取提高商品售价减少销售量的办法增加利润,如果这种商品每件的销售价每提高1元,其每天的销售量就减少20件.
(1)当售价定为12元时,每天可售出________件;
(2)要使每天利润达到640元,则每件售价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,过B作一直线与CD相交于点E,过A作AF垂直BE于点F,过C作CG垂直BE于点G,在FA上截取FH=FB,再过H作HP垂直AF交AB于P.若CG=3.则△CGE与四边形BFHP的面积之和为 _________ .
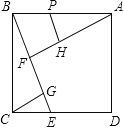
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com