
【题目】已知四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是射线
是射线![]() 上一点,点
上一点,点![]() 是射线
是射线![]() 上一点,且满足
上一点,且满足![]() .
.
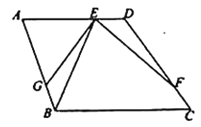
(1)如图,当点![]() 在线段
在线段![]() 上时,若
上时,若![]() ,在线段
,在线段![]() 上截取
上截取![]() ,联结
,联结![]() .求证:
.求证:![]() ;
;
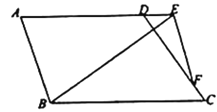
(2)如图,当点![]() 在线段
在线段![]() 的延长线上时,若
的延长线上时,若![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(3)记![]() 与
与![]() 交于点
交于点![]() ,在(2)的条件下,若
,在(2)的条件下,若![]() 与
与![]() 相似,求线段
相似,求线段![]() 的长.
的长.
【答案】(1)证明见详解;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)证明△EGB≌△FDE,根据全等三角形的性质即可证明.
(2) H为BC上一点,使四边形ABHD为等腰梯形,连接DH,作BI⊥AD于点I,作HJ⊥AD于点J,作DK⊥BC于点K,根据∠A=∠ADH=∠DHC,∠ABC=∠BHD=∠HDC+∠C∠ABC=2∠C,得到∠HDC=∠C,由![]() ,得到HD=HC=AB=3,AI=DJ=HK=1,
,得到HD=HC=AB=3,AI=DJ=HK=1,
则![]() ,求出
,求出![]() 作∠ENF=∠A,证明△DFN∽△DHC,又△NEF∽△ABE,根据相似三角形的性质得到
作∠ENF=∠A,证明△DFN∽△DHC,又△NEF∽△ABE,根据相似三角形的性质得到![]()
DE=x-4![]()
![]() ,代入
,代入![]() ,即可求出
,即可求出![]() 关于
关于![]() 的函数关系式及其定义域;
的函数关系式及其定义域;
(3) 根据△EMF∽△EMF,得到∠AEB=∠EFM=∠EFN,则∠AEB=![]() ∠EDC=
∠EDC=![]() ∠C,
∠C,
在AE上截取PE=BP,∠AEB=∠PBE=![]() ∠APB,证明△APB∽△HDC,根据相似三角形的性质得到△ABP的三边比为
∠APB,证明△APB∽△HDC,根据相似三角形的性质得到△ABP的三边比为![]() ,即可求出BP=PE=
,即可求出BP=PE=![]() ,即可求出线段
,即可求出线段![]() 的长.
的长.
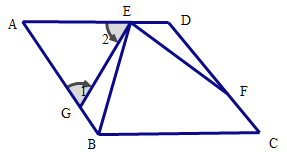
(1)证明:∵AD∥BC
∴∠A+∠ABC=180°,∠ADC+∠C=180°,
又∵∠A+∠1+∠2=180°,
又∵∠1=∠2
∴∠ABC=2∠1.
且∠ABC=2∠C,∴∠C=∠1,
∵∠BGE+∠1=180°
∴∠ADC=∠BGE,
∵∠A+∠ABE+∠AEB=180°,∠AEB+∠BEF+∠DEF=180°,
且∠A=∠BEF
∴∠ABE=∠DEF
∵AB=AD,AG=AE
∴BG=DE
∴△EGB≌△FDE
∴GE=DF.
(2)H为BC上一点,使四边形ABHD为等腰梯形,连接DH,作BI⊥AD于点I,作HJ⊥AD于点J,作DK⊥BC于点K,
易得∠A=∠ADH=∠DHC,∠ABC=∠BHD=∠HDC+∠C
又∵∠ABC=2∠C,
∴∠HDC=∠C
∵![]() ,
,
∴HD=HC=AB=3,AI=DJ=HK=1,
∴![]()
∴![]()

作∠ENF=∠A,
∴∠DHC=∠A=∠ENF,
∵∠NDF=∠C,
∴△DFN∽△DHC,
又∵△NEF∽△ABE
∴![]()
∴DE=x-4
∴![]()
![]()
![]() ,
,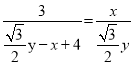
∴![]()
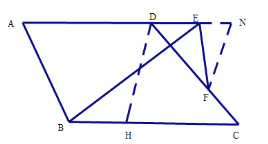
(3)∵△EMF与△ABE相似,
此时只有△EMF∽△EMF
∴∠AEB=∠EFM=∠EFN
∴∠AEB=![]() ∠EDC=
∠EDC=![]() ∠C
∠C
解△ABE,在AE上截取PE=BP,
∴∠AEB=∠PBE=![]() ∠APB
∠APB
∴∠APB=∠C
∴△APB∽△HDC,
∴△ABP的三边比为![]() ,
,
∴BP=PE=![]()
∴AE=AP+PE=![]() .
.



 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,点
,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() ,
,![]() 两点重合),连接
两点重合),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
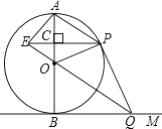
(1)求证:直线![]() 为
为![]() 的切线;
的切线;
(2)若直径![]() 的长为4.
的长为4.
①当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;
②当![]() ________时,四边形
________时,四边形![]() 为菱形.
为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
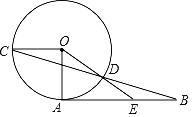
【题目】如图,AB是⊙O的切线,OA,OC是⊙O的半径,且OC∥AB,连接BC交⊙O于点D,点D恰为BC的中点,连接OD并延长,交AB于点E.
(1)求∠B的度数;
(2)求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某书店以![]() 元的价格购进一批科普书进行销售,物价局根据市场行情规定,销售单价不低于
元的价格购进一批科普书进行销售,物价局根据市场行情规定,销售单价不低于![]() 元且不高于
元且不高于![]() 元.在销售中发现,该科普书的每天销售数量
元.在销售中发现,该科普书的每天销售数量![]() (本)与销售单价
(本)与销售单价![]() (元)之间存在某种函数关系,对应如下:
(元)之间存在某种函数关系,对应如下:
销售单价 |
|
|
|
|
|
销售数量 |
|
|
|
|
|
(1)用你所学过的函数知识,求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)请问该科普书每天利润![]() (元)的最大值是多少?
(元)的最大值是多少?
(3)如果该科普书每天利润必须不少于![]() 元,试求出每天销售数量
元,试求出每天销售数量![]() 最少为多少本?
最少为多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q先以2![]() cm/s的速度沿A→O的路线向点O运动,然后再以2cm/s的速度沿O→D的路线向点D运动,当P、Q到达终点时,整个运动随之结束,设运动时间为t秒.
cm/s的速度沿A→O的路线向点O运动,然后再以2cm/s的速度沿O→D的路线向点D运动,当P、Q到达终点时,整个运动随之结束,设运动时间为t秒.
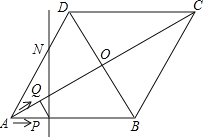
(1)在点P在AB上运动时,判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①直接写出当△PQM是直角三角形时t的取值范围;
②是否存在这样的t,使△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,某地的计价规则如表:
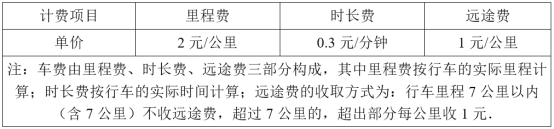
小李与小张分别从不同地点,各自同时乘坐滴滴快车,到同一地点相见,已知到达约定地点时他们的实际行车里程分别为7公里与9公里,两人付给滴滴快车的乘车费相同.其中一人先到达约定地点,他等候另一人的时间等于他自己实际乘车时间,且恰好是另一人实际乘车时间的一半,则小李的乘车费为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.

(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com