
【题目】如图,在矩形ABCD中,AB=6,AD=8,P是AD上的动点,PE⊥AC,PF⊥BD于F,求PE+PF的值.

【答案】![]() .
.
【解析】
根据矩形的性质和三角形的面积求出S△AOD=S△DOC=S△AOB=S△BOC=![]() S矩形ABCD=
S矩形ABCD=![]() ×6×8=12,根据勾股定理求出BD,求出AO、DO、根据三角形面积公式求出即可.
×6×8=12,根据勾股定理求出BD,求出AO、DO、根据三角形面积公式求出即可.
解:连接OP,
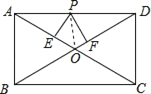
∵四边形ABCD是矩形,
∴∠DAB=90°,AC=2AO=2OC,BD=2BO=2DO,AC=BD,
∴OA=OD=OC=OB,
∴S△AOD=S△DOC=S△AOB=S△BOC=![]() S矩形ABCD=
S矩形ABCD=![]() ×6×8=12,
×6×8=12,
在Rt△BAD中,由勾股定理得:BD=![]() =10,
=10,
∴AO=OD=5,
∵S△APO+S△DPO=S△AOD,
∴![]() ×AO×PE+
×AO×PE+![]() ×DO×PF=12,
×DO×PF=12,
∴5PE+5PF=24,
∴PE+PF=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】阅读下列材料并解决有关问题:
我们知道,|m|= .现在我们可以用这一结论来化简含有绝对值的代
.现在我们可以用这一结论来化简含有绝对值的代
数式,如化简代数式|m+1|+|m﹣2|时,可令 m+1=0 和 m﹣2=0,分别求得 m=﹣1,m=2(称﹣1,2 分别为|m+1|与|m﹣2|的零点值).在实数范围内, 零点值 m=﹣1 和 m=2 可将全体实数分成不重复且不遗漏的如下 3 种情况:
(1)m<﹣1;(2)﹣1≤m<2;(3)m≥2.从而化简代数式|m+1|+|m﹣2| 可分以下 3 种情况:
(1)当 m<﹣1 时,原式=﹣(m+1)﹣(m﹣2)=﹣2m+1;
(2)当﹣1≤m<2 时,原式=m+1﹣(m﹣2)=3;
(3)当 m≥2 时,原式=m+1+m﹣2=2m﹣1.
综上讨论,原式=
通过以上阅读,请你解决以下问题:
(1)分别求出|x﹣5|和|x﹣4|的零点值;
(2)化简代数式|x﹣5|+|x﹣4|;
(3)求代数式|x﹣5|+|x﹣4|的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(6,c)三点,其中a,b,c满足关系式|a-2|+(b-3)2+![]() =0,
=0,
(1)求A.B.C的坐标;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点P,使三角形APC的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠B=90°,∠BCD=135°,且AB=3cm,BC=7cm,CD=5![]() cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为
cm,点M从点A出发沿折线A﹣B﹣C﹣D运动到点D,且在AB上运动的速度为![]() cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为
cm/s,在BC上运动的速度为1cm/s,在CD上运动的速度为![]() cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.
cm/s,连接AM、DM,当点M运动时间为_____(s)时,△ADM是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
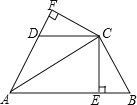
【题目】(本题8分) 已知,如图,AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=DC.
(1)求证:BE=DF;
(2)若AB=5,AD=3,求AE的长;
(3)若△ABC的面积是23,△ADC面积是18,则△BEC的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解某种车的耗油量,我们对这种车在高速公路以100km/h的速度做了耗油试验,并把试验的数据记录下来,制成下表:
汽车行驶时间t(h) | 0 | 1 | 2 | 3 | … | |
油箱剩余油量Q(L) | 100 | 94 | 88 | 82 | … |
(1)根据上表的数据,你能用t表示Q吗?试一试;
(2)汽车行驶6h后,油箱中的剩余油量是多少?
(3)若汽车油箱中剩余油量为52L,则汽车行驶了多少小时?
(4)若该种汽车油箱只装了36L汽油,汽车以100km/h的速度在一条全长700公里的高速公路上匀速行驶,请问它在中途不加油的情况下能从高速公路起点开到高速公路终点吗,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形OMN与正方形ABCD,半径OM与边AB重合,弧MN的长等于AB的长,已知AB=2,扇形OMN沿着正方形ABCD逆时针滚动到点O首次与正方形的某顶点重合时停止,则点O经过的路径长 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD,点E在边AD上,连接BE将△ABE沿BE翻折,得到△MBE,且点M是CD中点,取BM中点N,点P为线段BE上一动点,连接PN,PM,若AD长为2,则PM+PN的最小值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com