
【题目】如图所示,在![]() 中,
中,![]() ,
,![]() ,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于
,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N再分别以MN为圆心,大于![]() 的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的有________.
①AD是![]() 的平分线;②
的平分线;②![]() ;③点D在AB的中垂线上;④
;③点D在AB的中垂线上;④![]()

科目:初中数学 来源: 题型:
【题目】已知,如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(﹣1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
(1)求抛物线的解析式;
(2)求直线BC的解析式;
(3)求△MCB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD
(1)求证:△ABD≌△BCE.
(2)求证:AC是线段ED的垂直平分线.
(3)△DBC是等腰三角形吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在直角坐标系中,点A的坐标为(1,0),以OA为边在第一象限内作正方形OABC,点D是x轴正半轴上一动点(OD>1),连接BD,以BD为边在第一象限内作正方形DBFE,设M为正方形DBFE的中心,直线MA交y轴于点N.如果定义:只有一组对角是直角的四边形叫做损矩形.
(1)试找出图1中的一个损矩形;
(2)试说明(1)中找出的损矩形的四个顶点一定在同一个圆上;
(3)随着点D位置的变化,点N的位置是否会发生变化?若没有发生变化,求出点N的坐标;若发生变化,请说明理由;
(4)在图②中,过点M作MG⊥y轴于点G,连接DN,若四边形DMGN为损矩形,求D点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图三角形ABC中,AB=3,AC=4,以BC为边向三角形外作等边三角形BCD,连AD,则当∠BAC=_____度时,AD有最大值_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 地将一批物资运往
地将一批物资运往![]() 地,两车离
地,两车离![]() 地的距离
地的距离![]() (千米)与其相关的时间
(千米)与其相关的时间![]() (小时)变化的图像如图所示.读图后填空:
(小时)变化的图像如图所示.读图后填空:
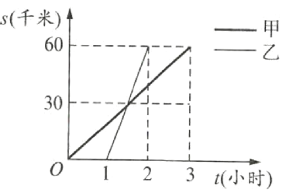
(1)![]() 地与
地与![]() 地之间的距离是______千米;
地之间的距离是______千米;
(2)甲车由![]() 地前往
地前往![]() 地时所对应的
地时所对应的![]() 与
与![]() 的函数解析式及定义域是__________;
的函数解析式及定义域是__________;
(3)甲车由![]() 地前往
地前往![]() 地比乙车由
地比乙车由![]() 地前往
地前往![]() 地多用了______小时.
地多用了______小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,过格点A、B、C作一圆弧.
(1)弧AC的长为_____(结果保留π);
(2)点B与图中格点的连线中,能够与该圆弧相切的连线所对应的格点的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c经过A(﹣1,0)、B(3,0)两点.
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<3时,求y的取值范围;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com