分析:可将不熟悉的“求三个二次根式和的最小值”的问题转化为熟悉的“求三条线段和的最小值“的问题.若A的坐标为(-3,2),B的坐标为(x,0),C的坐标为(0,y),D的坐标为(1,2),则根据勾股定理可得AB=
,BC=
,CD=
,从而得到原式=AB+BC+CD,只需求出AB+BC+CD的最小值就可解决问题.
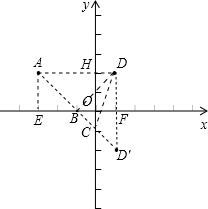
解答:解:如图,A的坐标为(-3,2),D的坐标为(1,2),点B在x轴上,点C在y轴上,
过点A作AE⊥x轴于E,过点D作DF⊥x轴于F,延长DF到点D′,使得FD′=FD,
连接AD交y轴于点H,连接AB、BC、CD、BD、BD′、AD′,
则DH⊥y轴,AD⊥DD′,BD=BD′,点D′的坐标为(1,-2).
设B的坐标为(x,0),C的坐标为(0,y),
在Rt△AEB中,
∵AE=2,BE=
=
,
∴AB=
=
=
.
在Rt△BOC中,
∵OB=
,OC=
,
∴BC=
=
.
在Rt△DHC中,
∵DH=1,CH=
,
∴CD=
=
=
.
∴原式=AB+BC+CD.
根据两点之间线段最短可得:
当B、C、D三点共线时,BC+CD最短,等于BD长
此时AB+BC+CD的最小值等于AB+BD.
∵BD=BD′,∴AB+BD=AB+BD′.
根据两点之间线段最短可得:
当A、B、D′三点共线时,AB+BD′最短,等于AD′长.
设直线AD′的解析式为y=kx+b,
则
.
解得:
.
∴直线AD′的解析式为y=-x-1.
当x=0时,y=-1;当y=0时,x=-1.
∴当代数式
+
+
取得最小值时,x=-1,y=-1.
∴x+y=-2.
故答案为:-2.




 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 在△ABC中,tanA=
在△ABC中,tanA=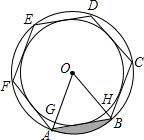 如图,两个同心圆的圆心为O,正六边形ABCDEF的顶点在大圆上,六条边分别与小圆相切,大圆的半径OA、OB分别与小圆相交于点G、H,正六边形的边长为2a.
如图,两个同心圆的圆心为O,正六边形ABCDEF的顶点在大圆上,六条边分别与小圆相切,大圆的半径OA、OB分别与小圆相交于点G、H,正六边形的边长为2a.
