
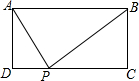
 如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5.
如图,矩形ABCD中,AD=2,AB=5,P为CD边上的动点,当△ADP与△BCP相似时,DP=1或4或2.5. 分析 需要分类讨论:△APD∽△PBC和△PAD∽△PBC,根据该相似三角形的对应边成比例求得DP的长度.
解答 解:①当△APD∽△PBC时,$\frac{AD}{PC}$=$\frac{PD}{BC}$,
即$\frac{2}{5-PD}$=$\frac{PD}{2}$,
解得:PD=1,或PD=4;
②当△PAD∽△PBC时,$\frac{AD}{BC}$=$\frac{PD}{PC}$,即$\frac{2}{2}$=$\frac{PD}{5-PD}$,
解得:DP=2.5.
综上所述,DP的长度是1或4或2.5.
故答案是:1或4或2.5.
点评 本题考查了矩形的性质,相似三角形的判定与性质.对于动点问题,需要分类讨论,以防漏解.


科目:初中数学 来源: 题型:解答题
| 月份 | 用水量(m3) | 收费(元) |
| 9 | 5 | 7.5 |
| 10 | 9 | 27 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )
如图所示,将一个透明的圆柱形玻璃容器(不计壁厚)中装入体积为容器一半容积的水,当水平放置该容器时,水面的形状为( )| A. | 圆 | B. | 椭圆 | ||
| C. | 一般的平行四边形 | D. | 矩形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
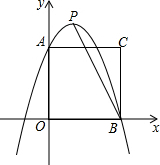 如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)
如图所示,将一边长为3的正方形放置到平面直角坐标系中,其顶点A、B均落在坐标轴上,一抛物线过点A、B,且顶点为P(1,4)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com