
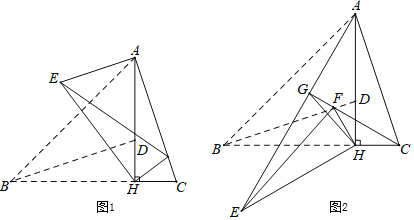
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 于点H,点D在AH上,且
于点H,点D在AH上,且![]() ,连接BD.
,连接BD.
![]() 如图1,将
如图1,将![]() 绕点H旋转,得到
绕点H旋转,得到![]() 点B、D分别与点E、F对应
点B、D分别与点E、F对应![]() ,连接AE,当点F落在AC上时
,连接AE,当点F落在AC上时![]() 不与C重合
不与C重合![]() ,求AE的长;
,求AE的长;
![]() 如图2,
如图2,![]() 是由
是由![]() 绕点H逆时针旋转
绕点H逆时针旋转![]() 得到的,射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
得到的,射线CF与AE相交于点G,连接GH,试探究线段GH与EF之间满足的等量关系,并说明理由.
【答案】(1)证明见解析;(2)(I)AE=![]() ;(II)
;(II)![]() .
.
【解析】
(1)先根据tanC=3,求出AH=3,CH=1,然后根据△EHA∽△FHC,得到,HP=3AP,AE=2AP,最后用勾股定理即可;
(2)先判断出△AGQ∽△CHQ,得到![]() ,然后判断出△AQC∽△GQH,用相似比即可.
,然后判断出△AQC∽△GQH,用相似比即可.
(1)如图,
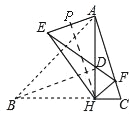
在Rt△AHC中,
∵tanC=3,
∴![]() =3,
=3,
设CH=x,
∴BH=AH=3x,
∵BC=4,
∴3x+x=4,
∴x=1,
∴AH=3,CH=1,
由旋转知,∠EHF=∠BHD=∠AHC=90°,EH=AH=3,CH=DH=FH,
∴∠EHF+∠AHF=∠AHC+∠AHF,
∴∠EHA=∠FHC,![]() =1,
=1,
∴△EHA∽△FHC,
∴∠EAH=∠C,
∴tan∠EAH=tanC=3,
过点H作HP⊥AE,
∴HP=3AP,AE=2AP,
在Rt△AHP中,AP2+HP2=AH2,
∴AP2+(3AP)2=9,
∴AP=![]() ,
,
∴AE=![]() ;
;
(2)如图1,
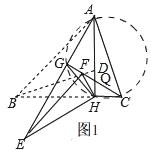
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴HD=HF,∠AHF=30°
∴∠CHF=90°+30°=120°,
由(1)有,△AEH和△FHC都为等腰三角形,
∴∠GAH=∠HCG=30°,
∴CG⊥AE,
∴点C,H,G,A四点共圆,
∴∠CGH=∠CAH,
设CG与AH交于点Q,
∵∠AQC=∠GQH,
∴△AQC∽△GQH,
∴![]() ,
,
∵△EHF是由△BHD绕点H逆时针旋转30°得到,
∴EF=BD,
由(1)知,BD=AC,
∴EF=AC
∴![]() =2,
=2,
即:EF=2HG,


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已如抛物线y=-x2+3x+m,其中m为常数
(I)当抛物线经过点(3,5)时,求该抛物线的解析式。
(II)当抛物线与直线y=x+3m只有一个交点时,求该抛物线的解析式。
(III)当0≤x≤4时,试通过m的取值范围讨论抛物线与直线y=x+2的公共点的个数的情况
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为[x].即当n为非负整数时,若n﹣![]() ≤x<n+
≤x<n+![]() ,则[x]=n.如:[2.9]=3;[2.4]=2;……根据以上材料,解决下列问题:
,则[x]=n.如:[2.9]=3;[2.4]=2;……根据以上材料,解决下列问题:
(1)填空[1.8]= ,[![]() ]= ;
]= ;
(2)若[2x+1]=4,则x的取值范围是 ;
(3)求满足[x]=![]() x﹣1的所有非负实数x的值.
x﹣1的所有非负实数x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)“2015扬州鉴真国际半程马拉松”的赛事共有三项:A、“半程马拉松”、B、“10公里”、C、“迷你马拉松”。小明和小刚参加了该项赛事的志愿者服务工作,组委会随机将志愿者分配到三个项目组
(1)小明被分配到“迷你马拉松”项目组的概率为
(2)求小明和小刚被分配到不同项目组的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“校园安全”受到全社会的广泛关注,我市某中学对部分学生就校园安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:

(1)接受问卷调查的学生共有_______人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_______°;
(2)请补全条形统计图;
(3)若该中学共有学生1800人,请根据上述调查结果,估计该中学学生中对校园安全知识 达到“了解”和“基本了解”程度的总人数;
查看答案和解析>>
科目:初中数学 来源: 题型:
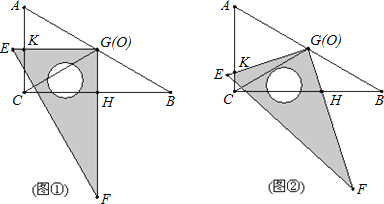
【题目】把两个全等的直角三角板ABC和EFG叠放在一起,使三角板EFG的直角顶点G与三角板ABC的斜边中点O重合,其中∠B=∠F=30°,斜边AB和EF长均为4.
(1)当 EG⊥AC于点K,GF⊥BC于点H时(如图①),求GH:GK的值.
(2) 现将三角板EFG由图①所示的位置绕O点沿逆时针方向旋转,旋转角α满足条件:0°<α<30°(如图②),EG交AC于点K ,GF交BC于点H,GH:GK的值是否改变?证明你发现的结论;
(3)三角板EFG由图①所示的位置绕O点逆时针旋转一周,是否存在某位置使△BFG是等腰三角形,若存在,请直接写出相应的旋转角α(精确到0.1°);若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某茶叶销售商计划将m罐茶叶按甲、乙两种礼品盒包装出售,其中甲种礼品盒每盒装4罐,每盒售价240元;乙种礼品盒每盒装6罐,每盒售价300元,恰好全部装完.已知每罐茶叶的成本价为30元,设甲种礼品盒的数量为x盒,乙种礼品盒的数量为y盒.
(1)当m=120时.
①求y关于x的函数关系式.
②若120罐茶叶全部售出后的总利润不低于3000元,则甲种礼品盒的数量至少要多少盒?
(2)若m罐茶叶全部售出后平均每罐的利润恰好为24元,且甲、乙两种礼品盒的数量和不超过69盒,求m的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
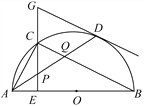
【题目】如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是![]() 的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
的中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论:①∠BAD=∠ABC;②GP=GD;③点P是△ACQ的外心,其中结论正确的是________(只需填写序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com