
| A. | 9000(单位) | B. | 8000(单位) | C. | 1000(单位) | D. | 18000(单位) |
分析 由需求函数为x=-900P+45000,可知单位产品的变动价格为P,利用需求量乘变动价格得出收入,减去固定成本和变动成本得出二次函数解析式,进一步利用二次函数的性质求得答案即可.
解答 解:由题意可知收入=P×x=P(-900P+45000)=45000P-900P2,
利润=(45000P-900P2)-10(-900P+45000)-270000=-900(P-30)2+90000,
当价格P=30元时,利润90000元为最大利润.
当P=30时,x=-900P+45000=18000.
故选:D.
点评 此题考查二次函数的实际运用,理解题意,利用基本的数量关系列出函数是解决问题的关键.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
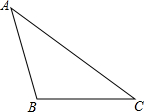 如图,已知△ABC,请按下列要求作图:
如图,已知△ABC,请按下列要求作图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
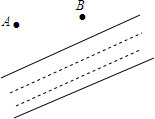 如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.
如图,小河边有两个村庄A,B,要在河边建一自来水厂向A村和B村供水.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
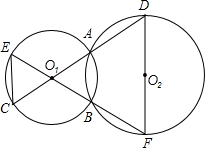 如图,⊙O1和⊙O2都经过A、B两点,过A点的直线CD与⊙O1交于点C,与⊙O2交于点D,过B点的直线EF与⊙O1交于点E,与⊙O2交于点F.求证:EF∥DF.
如图,⊙O1和⊙O2都经过A、B两点,过A点的直线CD与⊙O1交于点C,与⊙O2交于点D,过B点的直线EF与⊙O1交于点E,与⊙O2交于点F.求证:EF∥DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com