
 如图,在△ABC中,∠C=90°,AB=10,AC=8,
如图,在△ABC中,∠C=90°,AB=10,AC=8, 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开与旗杆底部相距5米后,发现下端刚好接触地面.请你求出旗杆的高度.
如图所示,小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开与旗杆底部相距5米后,发现下端刚好接触地面.请你求出旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:
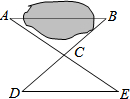 如图,有一池塘,要测量池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长至E,使CE=AC,连结BC并延长至D,使CD=BC,连结DE,根据△ABC≌△EDC可知,量出DE的长,就是A、B的距离,这里△ABC≌△EDC的依据是( )
如图,有一池塘,要测量池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C,连结AC并延长至E,使CE=AC,连结BC并延长至D,使CD=BC,连结DE,根据△ABC≌△EDC可知,量出DE的长,就是A、B的距离,这里△ABC≌△EDC的依据是( )| A、SAS | B、ASA |
| C、AAS | D、SSS |
查看答案和解析>>
科目:初中数学 来源: 题型:
| x | 0 | 0.5 | 1 | 1.5 | 2 |
| x2-bx-c | -15 | -8.75 | -2 | 5.25 | 13 |
| A、0.25 | B、0.75 |
| C、1.25 | D、1.75 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com