
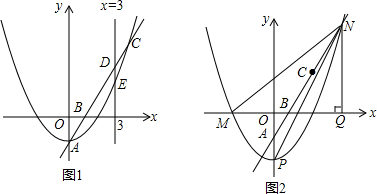
 在平面直角坐标系中,一个二次函数的图象经过点A(1,0)、B(3,0)两点.
在平面直角坐标系中,一个二次函数的图象经过点A(1,0)、B(3,0)两点.分析 (1)根据函数值相等的两点关于对称轴对称,可得答案;
(2)根据抛物线与x轴的交点坐标,可得交点式解析式,根据两组对边对应成比例且夹角相等的两个三角形相似,可得关于a的方程,根据解方程,可得答案.
解答 解:(1)由A(1,0)、B(3,0)关于对称轴对称,得
对称轴为直线:x=2,
故答案为:x=2;
(2)∵A(1,0)、B(3,0),
∴设这个二次函数的表达式y=a(x-1)(x-3)
当x=0时,y=3a,当x=2时,y=-a
∴C(0,3a),D(2,-a),∴OC=|3a|.
∵A(1,0)、E(2,0),∴OA=1,EB=1,DE=|-a|=|a|.
在△AOC与△DEB中,∵∠AOC=∠DEB=90°,
∴当$\frac{AO}{DE}$=$\frac{OC}{EB}$时,△AOC∽△DEB.∴$\frac{1}{|3a|}$=$\frac{|a|}{1}$时,解得a=$\frac{\sqrt{3}}{3}$或a=-$\frac{\sqrt{3}}{3}$;
当$\frac{AO}{EB}$=$\frac{OC}{DE}$时,△AOC∽△BED,∴$\frac{1}{|3a|}$=$\frac{1}{|a|}$时,此方程无解,
综上所述,所求二次函数的表达式为:y=$\frac{\sqrt{3}}{3}$(x-1)(x-3)或y=-$\frac{\sqrt{3}}{3}$(x-1)(x-3),
即y=$\frac{\sqrt{3}}{3}$x2-$\frac{4\sqrt{3}}{3}$x+$\sqrt{3}$或y=-$\frac{\sqrt{3}}{3}$x2+$\frac{4\sqrt{3}}{3}$x-$\sqrt{3}$.
点评 本题考查了二次函数综合题,利用函数值相等的两点关于对称轴对称得出得出对称轴,利用相似三角形的判定得出关于a的方程是解题关键,要分类讨论,以防遗漏.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,观察图(1)中三棱柱有5个面,6个顶点,9条棱;四棱柱有6个面,8个顶点,12条棱;五棱柱有7个面,10个顶点,15条棱…由此推得
如图,观察图(1)中三棱柱有5个面,6个顶点,9条棱;四棱柱有6个面,8个顶点,12条棱;五棱柱有7个面,10个顶点,15条棱…由此推得查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
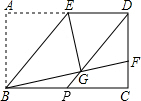 如图,矩形ABCD中,AB=6,BC=4$\sqrt{6}$,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.连接DG,并延长DG交BC于点P.
如图,矩形ABCD中,AB=6,BC=4$\sqrt{6}$,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.连接DG,并延长DG交BC于点P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
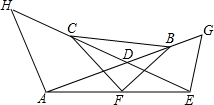 如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.
如图,已知AG与HE相交于点D,点B、C、F分别是DG、HD、AE的中点,若AH=AD,DE=EG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com