Question

【题目】若∠A与∠B的两边分别垂直，请判断这两个角的等量关系．

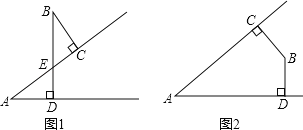
（1）如图1，∠A与∠B的关系是 ；如图2，∠A与∠B的关系是 ；

（2）若∠A与∠B的两边分别平行，试探索这两个角的等量关系，画图并证明你的结论．

Answer 1

【答案】（1）∠A=∠B，∠A+∠B=180°；（2）见解析

【解析】

试题分析：（1）根据垂直的量相等的角都等于90°，对顶角相等，所以∠A=∠B，同样根据垂直的量相等的角都等于90°，根据四边形的内角和等于360°，所以∠A+∠B=360°﹣90°﹣90°=180°．所以如果一个角的两边与另一个角的两边分别垂直，那么这两个角的关系是相等或互补；

（2）根据平行线的性质得到同位角相等，同旁内角互补即可得到结论．

（1）如图1，∠A=∠B，

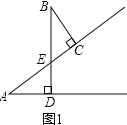
∵∠ADE=∠BCE=90°，∠AED=∠BEC，

∴∠A=180°﹣∠ADE﹣∠AED，

∠B=180°﹣∠BCE﹣∠BEC，

∴∠A=∠B，

如图2，∠A+∠B=180°；

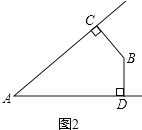
∴∠A+∠B=360°﹣90°﹣90°=180°．

∴∠A与∠B的等量关系是互补；

故答案为：∠A=∠B，∠A+∠B=180°；

（2）如图3，∠A=∠B，

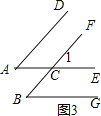
∵AD∥BF，∴∠A=∠1，

∵AE∥BG，∴∠1=∠B，

∴∠A=∠B；

如图4，∠A+∠B=180°，

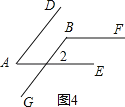
∵AD∥BG，

∴∠A=∠2，

∵AE∥BF，

∴∠2+∠B=180°，

∴∠A+∠B=180°．