
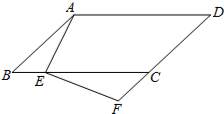
 如图,在?ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.求证:BE•EC=FC•CD.
如图,在?ABCD中,点E在BC边上,点F在DC的延长线上,且∠DAE=∠F.求证:BE•EC=FC•CD.  优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:选择题
 如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是( )
如图,AC是△ABC和△ADC的公共边,下列条件中不能判定△ABC≌△ADC的是( )| A. | AB=AD,∠2=∠1 | B. | AB=AD,∠3=∠4 | C. | ∠2=∠1,∠3=∠4 | D. | ∠2=∠1,∠B=∠D |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 今年,第十五号台风登陆江苏,A市接到台风警报时,台风中心位于A市正南方向104km的B处,正以16km/h的速度沿BC方向移动.
今年,第十五号台风登陆江苏,A市接到台风警报时,台风中心位于A市正南方向104km的B处,正以16km/h的速度沿BC方向移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)在平面直角坐标系中,点A的坐标是(0,2).在x轴上任取一点M,完成下列作图步骤:
(1)在平面直角坐标系中,点A的坐标是(0,2).在x轴上任取一点M,完成下列作图步骤:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式不正确的是( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列关系式不正确的是( )| A. | abc<0 | B. | a+b+c<0 | C. | 2a-b>0 | D. | 4a-b+c<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
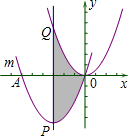 如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,且抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q.
如图,把抛物线y=$\frac{1}{2}$x2平移得到抛物线m,且抛物线m经过点A(-6,0)和原点O(0,0),它的顶点为P,它的对称轴与抛物线y=$\frac{1}{2}$x2交于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com