
【题目】如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;

(1)试判断四边形BECF是什么四边形?并说明理由.
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
【答案】(1)四边形BECF是菱形.证明见解析;(2)当∠A=45°时,菱形BECF是正方形.证明见解析.
【解析】
(1)根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE=EC,BF=FC,又因为CF=AE,可通过求证EC=AE得BE=EC=BF=FC,根据四边相等的四边形是菱形,证明四边形BECF是菱形;
(2)当∠A=45°时,可得∠EBF=90°,即可得到菱形BECF是正方形.
(1)四边形BECF是菱形.
证明:如图,∵BC的垂直平分线为EF,
∴BF=FC,BE=EC,
∴∠1=∠3,
∵∠ACB=90°,
∴∠1+∠2=90°,∠3+∠A=90°,
∴∠2=∠A,
∴EC=AE,
又∵CF=AE,BE=EC
∴BE=EC=CF=BF,
∴四边形BECF是菱形;
(2)当∠A=45°时,菱形BECF是正方形.
证明:∵∠A=45°,∠ACB=90°,
∴∠3=45°,
∴∠EBF=2∠3=90°,
∴菱形BECF是正方形.



科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c=0无实数根;③a-b+c≥0;④![]() 的最小值为3,其中正确结论的个数是( )
的最小值为3,其中正确结论的个数是( )
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC边上的点,点F在BC的延长线上,DE∥BC,若∠A=48°,∠1=54°,则下列正确的是( )

A. ∠2=48°B. ∠2=54°C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
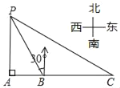
【题目】如图所示,某海盗船以20海里/小时的速度在某海域执行巡航任务,当海监船由西向东航行至A处使,测得岛屿P恰好在其正北方向,继续向东航行1小时到达B处,测得岛屿P在其北偏西30°方向,保持航向不变又航行2小时到达C处,求出此时海监船与岛屿P之间的距离(即PC的长,结果精确到0.1)(参考数据:![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE,则∠DEC的大小为( )

A. 78° B. 45° C. 60° D. 75°
查看答案和解析>>
科目:初中数学 来源: 题型:
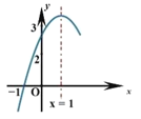
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,对称轴为直线
,对称轴为直线![]() ,
,![]() ,下列结论:①
,下列结论:①![]() ;②9a+3b+c=0;③若点
;②9a+3b+c=0;③若点![]() ,点
,点![]() 是此函数图象上的两点,则
是此函数图象上的两点,则![]() ;④
;④![]() .其中正确的个数( )
.其中正确的个数( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与x轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0),C(0,-3)
(1) 求抛物线的解析式;
(2) 若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值.
(3) 若点E在x轴上,点P在抛物线上,是否存在以A、C、E、P为顶点且以AC为一边的平行四边形?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com