
【题目】已知抛物线y=ax2+bx+c(b>a>0)与x轴最多有一个交点,现有以下四个结论:①该抛物线的对称轴在y轴左侧;②关于x的方程ax2+bx+c=0无实数根;③a-b+c≥0;④![]() 的最小值为3,其中正确结论的个数是( )
的最小值为3,其中正确结论的个数是( )
A.1 个B.2 个C.3 个D.4 个
【答案】C
【解析】
从抛物线与x轴最多一个交点及b>a>0,可以推断抛物线最小值最小为0,对称轴在y轴左侧,并得到b2-4ac≤0,从而得到①为正确,②错误;由x=-1及x=-2时y都大于或等于零可以得到③④正确.
∵b>a>0
∴-![]() <0,所以①正确;
<0,所以①正确;
∵抛物线与x轴最多有一个交点,
∴b2-4ac≤0,
∴关于x的方程ax2+bx+c=0有两个相等的实数根或无实数根;故②错误,
∵a>0及抛物线与x轴最多有一个交点,
∴x取任何值时,y≥0
∴当x=-1时,a-b+c≥0;所以③正确;
当x=-2时,4a-2b+c≥0,
a+b+c≥3b-3a,
a+b+c≥3(b-a),![]() ≥3,所以④正确.
≥3,所以④正确.
故选:C.


科目:初中数学 来源: 题型:
【题目】某市对一大型超市销售的甲、乙、丙3种大米进行质量检测.共抽查大米200袋,质量评定分为A、B两个等级(A级优于B级),相应数据的统计图如下:

根据所给信息,解决下列问题:
(1)a= ,b= ;
(2)已知该超市现有乙种大米750袋,根据检测结果,请你估计该超市乙种大米中有多少袋B级大米?
(3)对于该超市的甲种和丙种大米,你会选择购买哪一种?运用统计知识简述理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
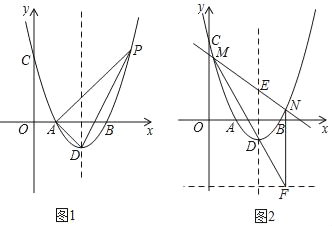
【题目】在平面直角坐标系中,抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,3),抛物线顶点为D点.
(1)求此抛物线解析式;
(2)如图1,点P为抛物线上的一个动点,且在对称轴右侧,若△ADP面积为3,求点P的坐标;
(3)在(2)的条件下,PA交对称轴于点E,如图2,过E点的任一条直线与抛物线交于M,N两点,直线MD交直线y=﹣3于点F,连结NF,求证:NF∥y轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
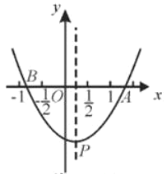
【题目】如图,抛物线y ax![]() bx c ( a, b, c 是常数,a 0 )与 x 轴交于A ,B 两点,顶点P(m,n),给出下列结论:①2a+c<0;②若
bx c ( a, b, c 是常数,a 0 )与 x 轴交于A ,B 两点,顶点P(m,n),给出下列结论:①2a+c<0;②若![]() ,
,![]() ,
,![]() 在抛物线上,则y1>y2>y3;③关于x的方程
在抛物线上,则y1>y2>y3;③关于x的方程![]() 有实数解,则
有实数解,则![]() ;④当
;④当![]() 时,△ABP为等腰直角三角形,正确的结论有( )个.
时,△ABP为等腰直角三角形,正确的结论有( )个.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:若存在实数对坐标(x,y)同时满足一次函数y=px+q和反比例函数y=![]() ,则二次函数y=px2+qxk为一次函数和反比例函数的“联姻”函数.
,则二次函数y=px2+qxk为一次函数和反比例函数的“联姻”函数.
(1)试判断(需要写出判断过程):一次函数y=x+3和反比例函数y=![]() 是否存在“联姻”函数,若存在,写出它们的“联姻”函数和实数对坐标.
是否存在“联姻”函数,若存在,写出它们的“联姻”函数和实数对坐标.
(2)已知:整数m,n,t满足条件t<n<8m,并且一次函数y=(1+n)x+2m+2与反比例函数y=![]() 存在“联姻”函数y=(m+t)x2+(10mt)x2015,求m的值.
存在“联姻”函数y=(m+t)x2+(10mt)x2015,求m的值.
(3)若同时存在两组实数对坐标[x1,y1]和[x2,y2]使一次函数y=ax+2b和反比例函数y=![]() 为“联姻”函数,其中,实数a>b>c,a+b+c=0,设
为“联姻”函数,其中,实数a>b>c,a+b+c=0,设![]() ,求L的取值范围.
,求L的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:一元二次方程(k-1)x2-2kx+k+2=0有两个不相等的实数根.
(1)求k的取值范围;
(2)设x1,x2是方程的两个不相等的实数根,且满足(k-1)x12+2kx2+k+2=4x1x2.求k的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2 是关于x的方程(x-2)(x-m)=(p-2)(p-m)的两个实数根.
(1)求x1,x2 的值;
(2)若x1,x2 是某直角三角形的两直角边的长,问当实数m,p满足什么条件时,此直角三角形的面积最大?并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在四边形ABFC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且CF=AE;

(1)试判断四边形BECF是什么四边形?并说明理由.
(2)当∠A的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com