
【题目】1号探测气球从海拔5m处出发,以1m/min的速度上升.与此同时,2号探测气球从海拔15m处出发,以0.5m/min的速度上升.两个气球都匀速上升了50min.设气球上升时间为x(x≥0).
(Ⅰ)根据题意,填写下表
上升时间/min | 10 | 30 | … | x |
1号探测气球所在位置的海拔/m | 15 | … | ||
2号探测气球所在位置的海拔/m | 30 | … |
(Ⅱ)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由.
(Ⅲ)当0≤x≤50时,两个气球所在位置的海拔最多相差多少米?
【答案】(1)35;![]() ;30;
;30;![]() ;(2)此时气球上升了20min,都位于海拔25m的高度;(3)当
;(2)此时气球上升了20min,都位于海拔25m的高度;(3)当![]() 时,y最大值为15.
时,y最大值为15.
【解析】
(Ⅰ)根据距离=速度×时间,分别计算即可得答案;(Ⅱ)根据上升的高度相同列方程可求出x的值,进而可求出两个气球所在高度;(Ⅲ)设两个气球在同一时刻所在的位置的海拔相差![]() m,由(Ⅱ)可知x=20时,两气球所在高度相同,当0≤x<20时,y=-0.5x+10,当20<x≤50时,y=0.5x-10,根据一次函数的性质分别求出最大值,比较即可得答案.
m,由(Ⅱ)可知x=20时,两气球所在高度相同,当0≤x<20时,y=-0.5x+10,当20<x≤50时,y=0.5x-10,根据一次函数的性质分别求出最大值,比较即可得答案.
(1)30×1+5=35,x+5,
10×0.5+15=20,0.5x+15,
故答案为:35;![]() ;20;
;20;![]()
(2)两个气球能位于同一高度.
根据题意,![]() ,
,
解得![]() ,
,
∴![]() .
.
答:能位于同一高度,此时气球上升了20min,都位于海拔25m的高度.
(3)设两个气球在同一时刻所在的位置的海拔相差ym
由(Ⅱ)可知x=20时,两气球所在高度相同,
∴①当0≤x<20时,由题意,可知1号探测气球所在位置始终低于2号气球,
则![]() .
.
∵-0.5<0,
∴y随x的增大而减小,
∴当![]() 时,y取得最大值10.
时,y取得最大值10.
②当20<x≤50时,由题意,可知1号探测气球所在位置始终高于2号气球,
则![]() .
.
∵0.5>0,
∴y随x的增大而增大,
∴当![]() 时,y取得最大值15.
时,y取得最大值15.
综上,当![]() 时,y最大值为15.
时,y最大值为15.
答:两个气球所在位置的海拔最多相差15m.


科目:初中数学 来源: 题型:
【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,连结AD,点E是AD的中点,连结BE并延长交CD于F点.
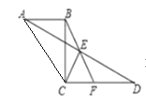
(1)请说明△ABE≌△DFE的理由;
(2)连结CE,AC,若CB⊥CD,AC=CD,∠D=30°,CD=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种学生用计算器,进价为每台20元,售价为每台30元时,每周可卖160台,如果每台售价每上涨2元,每周就会少卖20台,但厂家规定最高每台售价不能超过33元,当计算器定价为多少元时,商场每周的利润恰好为1680元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将边长为4的正方形纸片ABCD折叠,使得点A落在边CD的中点E处,折痕为FG,点F、G分别在边AD、BC上,则折痕FG的长度为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件40元,售价每件不低于60元且每件不高于80元.当售价为每件60元是,每个月可卖出100件;如果每件商品的售价每上涨1元,则每个月少卖2件.设每件商品的售价为![]() 元(
元(![]() 为正整数),每个月的销售利润为
为正整数),每个月的销售利润为![]() 元.
元.
(1)求![]() 与
与![]() 的函数关系式并直接写出自变量
的函数关系式并直接写出自变量![]() 的取值范围;
的取值范围;
(2)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?
(3)当每件商品定价为多少元使得每个月的利润恰为2250元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直径AB、CD相互垂直,P为弧BC上任意一点,连PC、PA、PD、PB,下列结论:①∠APC=∠DPE;②∠AED=∠DFA;③![]() ;其中正确的是( )
;其中正确的是( )
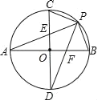
A. ①③B. 只有①C. 只有②D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是![]()
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是![]()
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M,N分别是正方形ABCD的边BC,CD上的点,且BM=CN, AM与BN交于点P,试探索AM与BN的关系.
(1)数量关系_____________________,并证明;
(2)位置关系_____________________,并证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com