
阅读理解:
学习了三角形全等的判定方法:“SAS”,“ASA”,“AAS”,“SSS”和直角三角形全等的判定方法“HL”后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA”的情形进行研究.
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D.
初步探究:
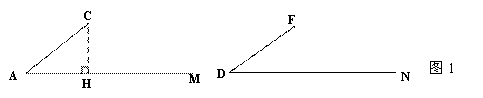
如图1,已知AC=DF, ∠A=∠D,过C作CH⊥射线AM于点H,对△ABC 的CB边进行分类,可分为“CB<CH,CB=CH,CH<CB<CA,”三种情况进行探究.
 |
深入探究:
第一种情况,当BC<CH时,不能构成△ABC和△DEF.
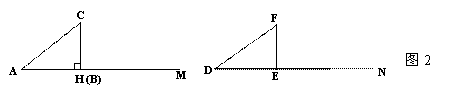
第二种情况,(1)如图2,当BC=CH时,在△ABC和△DEF中,AC=DF,BC=EF,∠A=∠D,根据 ,可以知道Rt△ABC≌Rt△DEF.
 |
第三种情况,(2)当CH<BC<CA时,△ABC和△DEF不一定全等.请你用尺规在图1的两个图形中分别补全△ABC和△DEF,使△DEF和△ABC不全等(表明字母,不写作法,保留作图痕迹).
(3)从上述三种情况发现,只有当BC=CH时,才一定能使△ABC≌△DEF. 除了上述三种情况外,BC边还可以满足什么条件,也一定能使△ABC≌△DEF?写出结论,并利用备用图证明.
 |
科目:初中数学 来源: 题型:
定义:如图1,平面上两条直线AB、CD相交于点O,对于平面内任意一点M,点M到直线AB、CD的距离分别为p、q,则称有序实数对(p,q)是点M的“距离坐标”.根据上述定义,“距离坐标”为(0,0)点有1个,即点O.
(1)“距离坐标”为(1,0)点有 个;
 | |||||
 | |||||
 | |||||
(2)如图2,若点M在过点O且与直线CD垂直的直线l上时,点M的“距离坐标”为
(p,q),且∠BOD=120°.请画出图形,并直接写出p,q的关系式;
(3)如图3,点M的“距离坐标”为(1,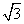 ),且∠AOB=30°,求OM的长.
),且∠AOB=30°,求OM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
课外阅读是提高学生素养的重要途径.某校为了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间t(小时).根据t的长短分为A,B,C,D四类,下 面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
面是根据所抽查的人数绘制的两幅不完整的统计图表.请根据图中提供的信息,解答下面的问题:
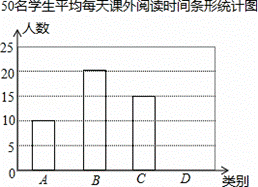 50名学生平均每天课外阅读时间统计表
50名学生平均每天课外阅读时间统计表
| 类别 | 时间t(小时) | 人数 |
| A | t<0.5 | 10 |
| B | 0.5≤t<1 | 20 |
| C | 1≤t<1.5 | 15 |
| D | t≥1.5 | a |
(1)本次调查的样本容量为 ;
(2)求表格中的a的值,并在图中补全条形统计图;
(3)该校现有1200名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,是根据媒体提供的消息 绘制的“宁波各大报刊发行量统计图”,那么发行量的众数是( )
绘制的“宁波各大报刊发行量统计图”,那么发行量的众数是( )
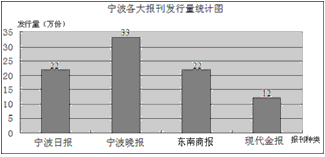
A.宁波晚报 B.宁波日报和东南商报 C.33万 D.22万
查看答案和解析>>
科目:初中数学 来源: 题型:
下列四个命题中:① 对角线相等的四边形是矩形;② 对角线互相平分的四边形是平行四边形;③ 对角线互相垂直的四边形是菱形;④ 对角线互相垂直且相等的四边形是正方形.其中正确的命题有( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com