已知：BE⊥CD于E，BE=DE
，BC=DA，
（1）求证：△BEC≌△DEA；
（2）求证：BC⊥FD．
学而优衔接教材南京大学出版社系列答案
小学课堂作业系列答案
金博士一点全通系列答案科目：初中数学 来源： 题型：
阅读理解：
学习了三角形全等的判定方法:“SAS”，“ASA”，“AAS”，“SSS”和直角三角形全等的判定方法“HL”后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA”的情形进行研究．
我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠A=∠D.
初步探究：
如图1，已知AC=DF, ∠A=∠D,过C作CH⊥射线AM于点H，对△ABC 的CB边进行分类，可分为“CB<CH，CB=CH，CH<CB<CA，”三种情况进行探究．
 |
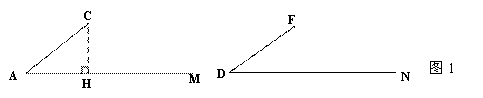深入探究：
第一种情况，当BC<CH时，不能构成△ABC和△DEF．
第二种情况，（1）如图2，当BC=CH时，在△ABC和△DEF中，AC=DF，BC=EF，∠A=∠D，根据 ，可以知道Rt△ABC≌Rt△DEF．
 |
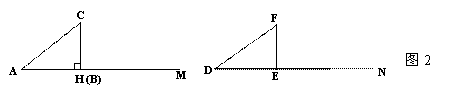第三种情况，（2）当CH<BC<CA时，△ABC和△DEF不一定全等．请你用尺规在图1的两个图形中分别补全△ABC和△DEF,使△DEF和△ABC不全等（表明字母，不写作法，保留作图痕迹）．
（3）从上述三种情况发现，只有当BC=CH时，才一定能使△ABC≌△DEF． 除了上述三种情况外，BC边还可以满足什么条件，也一定能使△ABC≌△DEF？写出结论,并利用备用图证明.
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
下列条件中，不能判断△ABC为直角三角形的是（）
A． a2=1，b2=2，c2=3 B． a：b：c=3：4：5
C． ∠A+∠B=∠C D． ∠A：∠B：∠C=3：4：5
查看答案和解析>>
科目：初中数学 来源： 题型：
在直线l上依次摆放着七个正方形（如图所示）．已知斜放置的三个正方形的面积分别是1，2，3，正放置的四个正方形的面积依次是S1，S2，S3，S4，则S1+S2+S3+S4=．
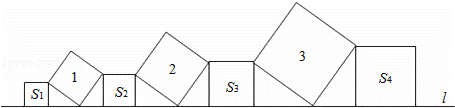
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，
，a、b为两个连续的整数，
＜
＜
，