
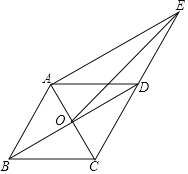
【题目】如图,平行四边形ABCD的对角线AC,BD相交于点O,延长CD到E,使DE=CD,连接AE.
(1)求证:四边形ABDE是平行四边形;
(2)连接OE,若∠ABC=60°,且AD=DE=4,求OE的长.
【答案】(1)见解析;(2)2![]() .
.
【解析】
(1)四边形ABCD是平行四边形,由平行四边形的性质,可得AB=DE, AB//DE ,则四边形ABDE是平行四边形;
(2)因为AD=DE=4,则AD=AB=4,四边形ABCD是菱形,由菱形的性质及解直角三角形可得AO=ABsin∠ABO=2,BO=ABcos∠ABO=2![]() , BD=4
, BD=4![]() ,则AE=BD,利用勾股定理可得OE.
,则AE=BD,利用勾股定理可得OE.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.
∵DE=CD,
∴AB=DE.
∴四边形ABDE是平行四边形;
(2)∵AD=DE=4,
∴AD=AB=4.
∴ABCD是菱形,
∴AB=BC,AC⊥BD,![]() ,
,![]() .
.
又∵∠ABC=60°,
∴∠ABO=30°.
在Rt△ABO中,![]() ,
,![]() .
.
∴![]() .
.
∵四边形ABDE是平行四边形,
∴AE∥BD,![]() .
.
又∵AC⊥BD,
∴AC⊥AE.
在Rt△AOE中,![]() .
.


科目:初中数学 来源: 题型:
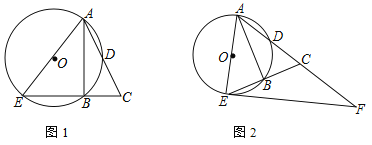
【题目】已知Rt△ABC中,AB是⊙O的弦,斜边AC交⊙O于点D,且AD=DC,延长CB交⊙O于点E.
(1)如图1,求证:AE=CE.
(2)如图2,过点E作⊙O的切线,交AC的延长线于点F.若CF=2CD,求sin∠CAB的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
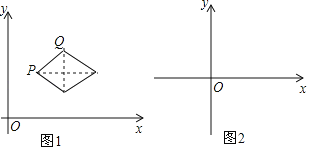
【题目】在平面直角坐标系xOy中,若P,Q为某个菱形相邻的两个顶点,且该菱形的两条对角线分别与x轴,y轴平行或重合,则称该菱形为点P,Q的“相关菱形”.图1为点P,Q的“相关菱形”的一个示意图.
已知点A的坐标为(1,4),点B的坐标为(b,0).
(1)若b=3,则R(﹣1,0),S(5,4),T(6,4)中能够成为点A,B的“相关菱形”顶点的是 ;
(2)若点A,B的“相关菱形”为正方形,求b的值;
(3)⊙B的半径为![]() ,点C的坐标为(2,4).若⊙B上存在点M,在线段AC上存在点N,使点M,N的“相关菱形”为正方形,请直接写出b的取值范围.
,点C的坐标为(2,4).若⊙B上存在点M,在线段AC上存在点N,使点M,N的“相关菱形”为正方形,请直接写出b的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列对于随机事件的概率的描述:
①抛掷一枚均匀的硬币,因为“正面朝上”的概率是0.5,所以抛掷该硬币100次时,就会有50次“正面朝上”;
②一个不透明的袋子里装有4个黑球,1个白球,这些球除了颜色外无其他差别.从中随机摸出一个球,恰好是白球的概率是0.2;
③测试某射击运动员在同一条件下的成绩,随着射击次数的增加,“射中9环以上”的频率总是在0.85附近摆动,显示出一定的稳定性,可以估计该运动员“射中9环以上”的概率是0.85
其中合理的有______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
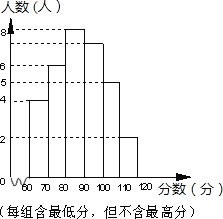
【题目】某中学部分同学参加全国初中数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分120分),并且绘制了“频率分布直方图”(如图).请回答:
(1)该中学参加本次数学竞赛的有多少名同学?
(2)如果成绩在90分以上(含90分)的同学获奖,那么该中学参赛同学的获奖率是多少?
(3)这次竞赛成绩的中位数落在哪个分数段内?
(4)图中还提供了其它信息,例如该中学没有获得满分的同学等等,请再写出两条信息.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,AC=BC=2,点P为BC边上的一个动点(不与点B,C重合).点P关于直线AC,AB的对称点分别为M,N,连接MN交AC于点E,交AB于点F.
(1)当点P为线段BC的中点时,求∠M的正切值.
(2)当点P在线段BC上运动时(不与B,C重合),连接AM,AN,求证:
①△AMN为等腰直角三角形;
②△AEF∽△BAM.

查看答案和解析>>
科目:初中数学 来源: 题型:
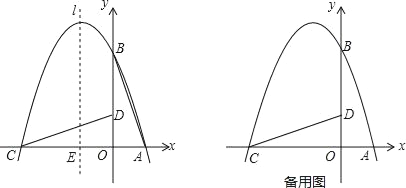
【题目】如图,在平面直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A、B、C.
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求以C、E、F为顶点三角形与△COD相似时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 坐标为
坐标为![]() ,点
,点![]() 在
在![]() 边上从点
边上从点![]() 运动到点
运动到点![]() ,以
,以![]() 为边作正方形
为边作正方形![]() ,连
,连![]() ,在点
,在点![]() 运动过程中,请探究以下问题:
运动过程中,请探究以下问题:

(1)![]() 的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
的面积是否改变,如果不变,求出该定值;如果改变,请说明理由;
(2)若![]() 为等腰三角形,求此时正方形
为等腰三角形,求此时正方形![]() 的边长.
的边长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com