
分析 (1)先画出函数y=x2-2x-3的图象,然后求得抛物线与x轴交点的坐标,最后根据函数图形回答即可;
(2)先判断出抛物线的开口方向,然后求得抛物线与x轴交点坐标,最后根据函数图象进行判断即可
解答 解:(1)设y=x2-2x-3,则y是x的二次函数.
∵a=1>0,
∴抛物线开口向上.
又∵当y=0时,x2-2x-3=0,解得x1=-1,x2=3,
∴由此得抛物线y=x2-2x-3的大致图象如图所示.
观察函数图象可知:当x<-1或x>3时,y>0.
∴x2-2x-3>0的解集是:x<-1或x>3.
故答案为:x<-1或x>3.
(2)设y=x2-4,则y是x的二次函数.
∵a=1>0,
∴抛物线开口向上.
又∵当y=0时,x2-4=0,解得x1=-2,x2=2,
∴由此得抛物线y=x2-4的大致图象如图所示.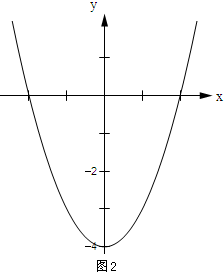
观察函数图象可知:当x<-2或x>2时,y>0.
∴x2-4>0的解集是:x<-2或x>2.
点评 本题主要考查的是二次函数与不等式组,利用函数图象确定出不等式组的解集是解题的关键.


 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源: 题型:解答题
| x | … | -1 | 0 | 1 | 2 | … |
| y1=2x+3 | … | 1 | 3 | 5 | 7 | … |
| y2=x2 | … | 1 | 0 | 1 | 4 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的半径为3cm,现准备将这个圆分成三个面积相等的三部分.请你设计至少四种方案(要求:1.有图形的分割示意图;2.图中标明关键而必要的数据;3.有简单的计算说明过程)
如图,⊙O的半径为3cm,现准备将这个圆分成三个面积相等的三部分.请你设计至少四种方案(要求:1.有图形的分割示意图;2.图中标明关键而必要的数据;3.有简单的计算说明过程)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
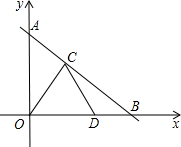 如图,直线y=kx+b与y轴交于点A,与x轴交于点B,边长为2的等边△COD的顶点C、D分别在线段AB、OB上,且DO=2DB.
如图,直线y=kx+b与y轴交于点A,与x轴交于点B,边长为2的等边△COD的顶点C、D分别在线段AB、OB上,且DO=2DB.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
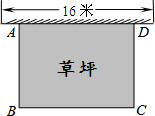 如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.则该矩形草坪BC边的长是( )
如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.则该矩形草坪BC边的长是( )| A. | 12 | B. | 18 | C. | 20 | D. | 12或20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com