
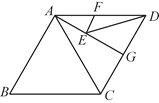
【题目】如图,在菱形ABCD中,AB=6,∠B=60°,点G是CD边的中点,点E、F分别是AG、AD上的两个动点,则EF+ED的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
【题目】一辆货车从百货大楼出发送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
![]()
(1)以百货大楼为原点,向东为正方向,1个单位长度表示1千米,请在数轴上标出小明、小红、小刚家的位置.(小明家用点![]() 表示,小红家用点
表示,小红家用点![]() 表示,小刚家用点
表示,小刚家用点![]() 表示)
表示)
(2)求这辆货车此次送货(从出发到返回百货大楼)总共走的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC边上的中点,两边PE,PF分别交AB,AC于点E,F,给出以下四个结论:

①AE=CF;②EF=AP;③2S四边形AEPF=S△ABC;④当∠EPF在△ABC内绕顶点P旋转时(点E不与A,B重合)有BE+CF=EF;上述结论中始终正确的序号有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
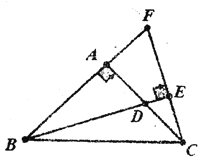
【题目】如图,等腰直角三角形ABC中,∠BAC=90°,D是AC的中点,EC⊥BD于E,交BA的延长线于F,若BF=12,则△BDC的面积是______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球.B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出刚好抽到同性别学生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
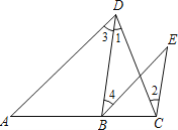
【题目】已知:如图,∠1=∠2,∠3=∠E,试说明:∠A=∠EBC,(请按图填空,并补理由,)
证明:∵∠1=∠2(已知),
∴______∥______,________
∴∠E=∠______,________
又∵∠E=∠3(已知),
∴∠3=∠______(等量代换),
∴______∥______(内错角相等,两直线平行),
∴∠A=∠EBC,________
查看答案和解析>>
科目:初中数学 来源: 题型:
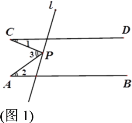
【题目】已知直线AB∥CD,点P为直线l上一点,尝试探究并解答:
(1)如图1,若点P在两平行线之间,∠1=23°,∠2=35°,则∠3= ;
(2)探究图1中∠1,∠2与∠3之间的数量关系,并说明理由;
(3)如图2,若点P在CD的上方,探究∠1,∠2与∠3之间有怎样的数量关系,并说明理由;
(4)如图3,若∠PCD与∠PAB的平分线交于点P1,∠DCP1与∠BAP1的平分线交于点P2,∠DCP2与∠BAP2的平分线交于点P3,…,∠DCPn-1与∠BAPn-1的平分线交于点Pn,若∠PCD=α,∠PAB=β,直接写出∠APnC的度数(用含α与β的代数式表示).


查看答案和解析>>
科目:初中数学 来源: 题型:
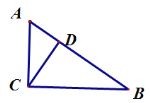
【题目】如图,已知AC⊥BC于C,CD⊥AB于D,BC=8,AC=6,CD=4.8,BD=6.4,AD=3.6.则:
(1)点A到直线CD的距离为_________;
(2)点A到直线BC的距离为_________;
(3)点B到直线CD的距离为_________;
(4)点B到直线AC的距离为_________;
(5)点C到直线AB的距离为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com