考点:有理数的混合运算
专题:
分析:(1)根据有理数的减法法则,减去一个数等于加上这个数的相反数进行计算即可;
(2)根据有理数的减法法则,减去一个数等于加上这个数的相反数进行计算即可;
(3)根据有理数的加法法则,进行计算即可;
(4)根据除以一个数等于乘以这个数的倒数进行计算即可;
(5)根据绝对值,有理数的加法法则,进行计算即可;
(6)根据乘法的交换律,先把4与0.25相乘,再进行计算即可;
(7)根据乘法的分配律进行计算即可;
(8)根据除以一个数等于乘以这个数的倒数进行计算即可;
(9)根据乘法的交换律进行计算即可;
(10)根据除以一个数等于乘以这个数的倒数进行计算即可;
(11)根据乘法的分配律进行计算即可.
解答:解:(1)(-72 )-25=(-72)+(-25)
=-(72+25)
=-97;
(2)0-(-8)=0+8
=8;
(3)(-13)+(-32)
=-(13+32)
=-45;
(4)
×0.5÷(-4)
=-
×
×
=-
;
(5)1+(-2)+|-3|-5
=1+(-2)+3+(-5)
=4+(-7)
=-3;
(6)(-4)×2×(-0.25)
=4×0.25×2
=2;
(7)(
+
-
)×(-12)
=12×
+12×
-12×
=5+8-9
=4;
(8)(-
)×(-1
)÷(-2
)
=-
×
×
=-
;
(9)(-5)×8×(-1
)×(-1.25)
=-8×1.25×5×
=-10×9
=-90;
(10)(-
)×(-
)÷(-1
)×3
=-
×
×
×3
=-1;
(11)(-27
)÷9-(
+
-
-
)×(-24)
=(-27-
)×
+24×
+24×
-24×
-24×
=-27×
-
×
+12+16-18-22
=-3-
-12
=-15
.
点评:本题考查了有理数的混合运算,注意:除以一个数等于乘以这个数的倒数,要熟练掌握.



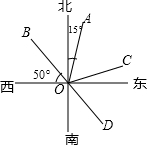 如图,OA的方向是北偏东15°,OB的方向是西偏北50°.
如图,OA的方向是北偏东15°,OB的方向是西偏北50°.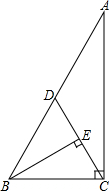 已知如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,连接CD,BE⊥CD于点E.AB=10,S△ABC=24.
已知如图,在Rt△ABC中,∠ACB=90°,点D是斜边AB的中点,连接CD,BE⊥CD于点E.AB=10,S△ABC=24.