
 如图1,在边长为2的等边△ABC中,⊙A与BC相切于点D,阴影部分的面积记作S1;如图2,最大圆半径r=1,阴影部分的面积记作S2,则S1与S2的大小关系是( )
如图1,在边长为2的等边△ABC中,⊙A与BC相切于点D,阴影部分的面积记作S1;如图2,最大圆半径r=1,阴影部分的面积记作S2,则S1与S2的大小关系是( )| A、S1>S2 |
| B、S1<S2 |
| C、S1=S2 |
| D、无法确定 |
| 3 |
| 3 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| π |
| 4 |
| ||
| 2 |
2
| ||
| 4 |
| π |
| 4 |


科目:初中数学 来源: 题型:
| A、这个地区从现在开始经过6至7天会发生降水 |
| B、这个地区未来10天内将会发生一次降水 |
| C、这个地区未来10天内发生降水比不发生降水的可能性大 |
| D、我们不能判断何时会有降水发生 |
查看答案和解析>>
科目:初中数学 来源: 题型:

| 2n |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
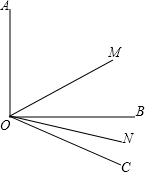 已知如图,OM平分∠AOC,ON平分∠BOC,若∠AOB=90°,∠BOC=30°
已知如图,OM平分∠AOC,ON平分∠BOC,若∠AOB=90°,∠BOC=30°查看答案和解析>>
科目:初中数学 来源: 题型:
| A、日光灯管厂要检测一批灯管的使用寿命,采用普查方式 |
| B、了解海门市每天的流动人口数,采用抽样调查方式 |
| C、了解海门市民对各类电视节目的喜爱情况,采用普查方式 |
| D、旅客上飞机前的安检,采用抽样调查方式 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图所示,关于该二次函数,下列说法中错误的是( )| A、函数有最小值 | ||
| B、当-1<x<2时,y>0 | ||
C、当x<
| ||
D、对称轴是直线x=
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com