
【题目】如图,抛物线y=ax2+bx+c经过点A(﹣3,0),B(1,0),C(0,﹣3).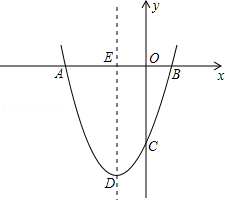
(1)求抛物线的解析式;
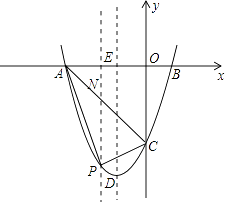
(2)若点P为第三象限内抛物线上的一点,设△PAC的面积为S,求S的最大值并求出此时点P的坐标;
(3)设抛物线的顶点为D,DE⊥x轴于点E,在y轴上是否存在点M,使得△ADM是直角三角形?若存在,请直接写出点M的坐标;若不存在,请说明理由.
【答案】
(1)
解:由于抛物线y=ax2+bx+c经过A(﹣3,0),B(1,0),可设抛物线的解析式为:y=a(x+3)(x﹣1),
将C点坐标(0,﹣3)代入,得:
a(0+3)(0﹣1)=﹣3,解得 a=1,
则y=(x+3)(x﹣1)=x2+2x﹣3,
所以抛物线的解析式为:y=x2+2x﹣3
(2)
解:过点P作x轴的垂线,交AC于点N.
设直线AC的解析式为y=kx+m,由题意,得
![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为:y=﹣x﹣3.
设P点坐标为(x,x2+2x﹣3),则点N的坐标为(x,﹣x﹣3),
∴PN=PE﹣NE=﹣(x2+2x﹣3)+(﹣x﹣3)=﹣x2﹣3x.
∵S△PAC=S△PAN+S△PCN,
∴S= ![]() PNOA
PNOA
= ![]() ×3(﹣x2﹣3x)
×3(﹣x2﹣3x)
=﹣ ![]() (x+
(x+ ![]() )2+
)2+ ![]() ,
,
∴当x=﹣ ![]() 时,S有最大值
时,S有最大值 ![]() ,此时点P的坐标为(﹣
,此时点P的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )
)
(3)
解:在y轴上是存在点M,能够使得△ADM是直角三角形.理由如下:
∵y=x2+2x﹣3=y=(x+1)2﹣4,
∴顶点D的坐标为(﹣1,﹣4),
∵A(﹣3,0),
∴AD2=(﹣1+3)2+(﹣4﹣0)2=20.
设点M的坐标为(0,t),分三种情况进行讨论:
①当A为直角顶点时,如图3①,
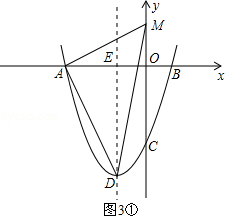
由勾股定理,得AM2+AD2=DM2,即(0+3)2+(t﹣0)2+20=(0+1)2+(t+4)2,
解得t= ![]() ,
,
所以点M的坐标为(0, ![]() );
);
②当D为直角顶点时,如图3②,
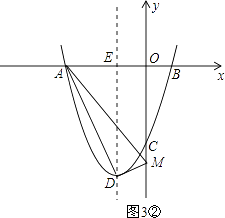
由勾股定理,得DM2+AD2=AM2,即(0+1)2+(t+4)2+20=(0+3)2+(t﹣0)2,
解得t=﹣ ![]() ,
,
所以点M的坐标为(0,﹣ ![]() );
);
③当M为直角顶点时,如图3③,
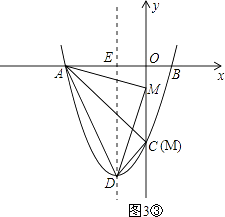
由勾股定理,得AM2+DM2=AD2,即(0+3)2+(t﹣0)2+(0+1)2+(t+4)2=20,
解得t=﹣1或﹣3,
所以点M的坐标为(0,﹣1)或(0,﹣3);
综可知,在y轴上存在点M,能够使得△ADM是直角三角形,此时点M的坐标为(0, ![]() )或(0,﹣
)或(0,﹣ ![]() )或(0,﹣1)或(0,﹣3)
)或(0,﹣1)或(0,﹣3)
【解析】(1)已知抛物线上的三点坐标,利用待定系数法可求出该二次函数的解析式;(2)过点P作x轴的垂线,交AC于点N,先运用待定系数法求出直线AC的解析式,设P点坐标为(x,x2+2x﹣3),根据AC的解析式表示出点N的坐标,再根据S△PAC=S△PAN+S△PCN就可以表示出△PAC的面积,运用顶点式就可以求出结论;(3)分三种情况进行讨论:①以A为直角顶点;②以D为直角顶点;③以M为直角顶点;设点M的坐标为(0,t),根据勾股定理列出方程,求出t的值即可.
【考点精析】通过灵活运用二次函数的图象和二次函数的性质,掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小即可以解答此题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
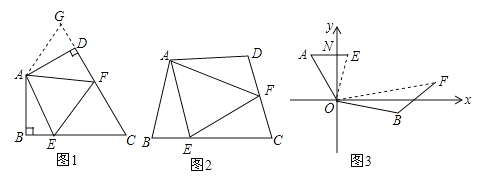
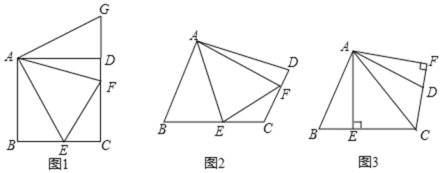
【题目】(1)问题背景:如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC,CD上的点,且∠EAF=60°,探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是延长FD到点G,使DG=BE,连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是_____________________;
(2)探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF=∠BAD,上述结论是否仍然成立,并说明理由;
(3)结论应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等.接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇与指挥中心O之间夹角∠EOF=70°,试求此时两舰艇之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB,CD相交于点O,作∠DOE=∠BOD,OF平分∠AOE.
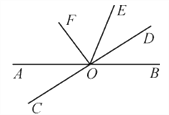
(1)判断OF与OD的位置关系;
(2)若∠AOC∶∠AOD=1∶5,求∠EOF的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形是将正三角形按一定规律排列,第 1 个图形中所有正三角形的个数有 1 个,第 2 个图形中所有正三角形的个数有 5 个,第 3 个图形中所有正三角形的个数有 17 个,则第 5 个图形中所有正三角形的个数有( )
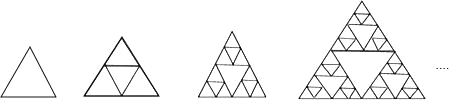
A. 160 B. 161 C. 162 D. 163
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图 1,四边形 ABCD 中,∠BAD=∠ADC=∠CBA=90°,AB=AD,点 E、F 分别在四边形 ABCD 的边 BC、CD 上,∠EAF=45°,点 G 在 CD 的延长线上,BE=DG,连接 AG,求证:EF=BE+FD.
(2)如图 2,四边形 ABCD 中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点 E、F 分别在边BC、CD 上,则当∠BAD=2∠EAF 时,仍有 EF=BE+FD 成立吗?说明理由.
(3)如图 3,四边形 ABCD 中,∠BAD≠90°,AB=AD,AC 平分∠BCD,AE⊥BC 于 E,AF⊥CD 交 CD 延长线于 F,若 BC=9,CD=4,则 CE= .(不需证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小兰:“小红,你上周买的笔和笔记本的价格是多少啊?”小红:“哦,…,我忘了!只记得先后买了两次,第一次买了5支笔和10本笔记本共花了42元钱,第二次买了10支笔和5本笔记本共花了30元钱.”请根据小红与小兰的对话,求得小红所买的笔和笔记本的价格分别是( )
A. 0.8元/支,2.6元/本 B. 1.2元/支,3.6元/本
C. 1.2元/支,2.6元/本 D. 0.8元/支,3.6元/本
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】本学期学校开展以“感受中华传统美德”为主题的研学活动,组织150名学生参观历史博物馆和民俗展览馆,每一名学生只能参加其中一项活动,共支付票款2000元,票价信息如下:
地点 | 票价 |
历史博物馆 | 10元/人 |
民俗展览馆 | 20元/人 |
(1)请问参观历史博物馆和民俗展览馆的人数各是多少人?
(2)若学生都去参观历史博物馆,则能节省票款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,东方红商场决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折,已知打折前,买6盒甲品牌粽子和3盒乙品牌粽子需660元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com