
【题目】小明和小亮在学习探索三角形全等时,碰到如下一题:如图1,若AC=AD,BC=BD,则△ACB与△ADB有怎样的关系? 


(1)请你帮他们解答,并说明理由.
(2)细心的小明在解答的过程中,发现如果在AB上任取一点E,连接CE、DE,则有CE=DE,你知道为什么吗?(如图2)
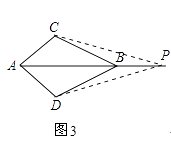
(3)小亮在小明说出理由后,提出如果在AB的延长线上任取一点P,也有第2题类似的结论.请你帮他画出图形,并写出结论,不要求说明理由.(如图3)
【答案】
(1)解:△ACB≌△ADB,理由如下:
如图1,∵在△ACB与△ADB中,
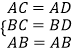 ,
,
∴△ACB≌△ADB(SSS)
(2)解:如图2,∵由(1)知,△ACB≌△ADB,则∠CAE=∠DAE.
∴在△CAE与△DAE中,
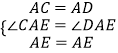 ,
,
∴△CAE≌△DAE(SAS),
∴CE=DE
(3)解:如图3,PC=PD.
理由同(2),△APC≌△APD(SAS),则PC=PD
【解析】(1)根据全等三角形的判定定理SSS证得△ACB≌△ADB;(2)由(1)中的全等三角形(△ACB≌△ADB)的对应角相等证得∠CAE=∠DAE,则由全等三角形的判定定理SAS证得△CAE≌△DAE,则对应边CE=DE;(3)同(2),利用全等三角形的对应边相等证得结论.


 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到设计方案有等腰三角形,正三角形,等腰梯形和菱形四种图形,你认为符合条件的是( )
A.等腰三角形
B.正三角形
C.等腰梯形
D.菱形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若P,Q是直线AB外不重合的两点,则下列说法不正确的是( )
A. 直线PQ可能与直线AB垂直
B. 直线PQ可能与直线AB平行
C. 过点P的直线一定能与直线AB相交
D. 过点Q只能画出一条直线与AB平行
查看答案和解析>>
科目:初中数学 来源: 题型:
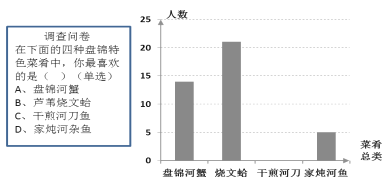
【题目】某数学兴趣小组在全校范围内随机抽取了50名同学进行“舌尖上的盘锦﹣﹣我最喜爱的盘锦特色菜肴”调查活动,将调查问卷整理后绘制成如图所示的不完整条形统计图:请根据所给信息解答以下问题:
(1)请补全条形统计图;
(2)若全校有3000名同学,请估计全校同学中最喜爱“盘锦河蟹”的同学有多少人?
(3)在此次调查活动中,有3男2女共5名工作人员,若从中随机选择2名负责调查问卷的发放和回收工作,请用列表或画树状图的方法,求出这2名工作人员恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中不正确的是( )
A. 一个数与它的倒数之积是1 B. 商为-1的两个数互为相反数
C. 一个数与它的相反数之商一定为-1 D. 积为1的两个数互为倒数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.求证: 
(1)FC=AD;
(2)AB=BC+AD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自学下面材料后,解答问题。
分母中含有未知数的不等式叫分式不等式。如:![]() 等 。那么如何求出它们的解集呢?
等 。那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负。其字母表达式为:
(1)若a>0 ,b>0 ,则![]() >0;若a<0 ,b<0,则
>0;若a<0 ,b<0,则![]() >0;
>0;
(2)若a>0 ,b<0 ,则![]() <0 ;若a<0,b>0 ,则
<0 ;若a<0,b>0 ,则![]() <0。
<0。
反之:(1)若![]() >0则
>0则![]()
(2)若![]() <0 ,则__________或_____________.
<0 ,则__________或_____________.
根据上述规律,求不等式![]() 的解集。
的解集。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com