
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() 、
、![]() 重合),在
重合),在![]() 同侧分别作等边
同侧分别作等边![]() 和等边
和等边![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() 、
、![]() ,以下五个结论:①
,以下五个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]() .一定成立的结论有______________;
.一定成立的结论有______________;
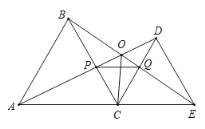
【答案】①②③⑤.
【解析】
①由于△ABC和△CDE是等边三角形,可知AC=BC,CD=CE,∠ACB=∠DCE=60°,从而证出△ACD≌△BCE,可推知AD=BE;
②由△ACD≌△BCE得∠CBE=∠DAC,加之∠ACB=∠DCE=60°,AC=BC,得到△CQB≌△CPA(ASA),再根据∠PCQ=60°推出△PCQ为等边三角形,又由∠PQC=∠DCE,根据内错角相等,两直线平行,可知②正确;
③根据②△CQB≌△CPA(ASA),可知③正确;
④根据∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,可知∠DQE≠∠CDE,可知④错误;
⑤由BC∥DE,得到∠CBE=∠BED,由∠CBE=∠DAE,得到∠AOB=∠OAE+∠AEO=60°可得出∠AOE=120°,再利用三角形相似以及等边三角形的知识可知⑤正确;
解:∵等边△ABC和等边△CDE,
∴AC=BC,CD=CE,∠ACB=∠DCE=60°,
∴∠ACB+∠BCD=∠DCE+∠BCD,即∠ACD=∠BCE,
在△ACD与△BCE中,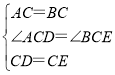 ,
,
∴△ACD≌△BCE(SAS),
∴AD=BE,
∴①正确;
∵△ACD≌△BCE,
∴∠CBE=∠DAC,
又∵∠ACB=∠DCE=60°,
∴∠BCD=60°,即∠ACP=∠BCQ,
又∵AC=BC,
∴△CQB≌△CPA(ASA),
∴CP=CQ,
又∵∠PCQ=60°可知△PCQ为等边三角形,
∴∠PQC=∠DCE=60°,
∴PQ∥AE
∴②正确;
∵△CQB≌△CPA,
∴AP=BQ
∴③正确;
∵AD=BE,AP=BQ,
∴AD-AP=BE-BQ,
即DP=QE,
∵∠DQE=∠ECQ+∠CEQ=60°+∠CEQ,∠CDE=60°,
∴∠DQE≠∠CDE,故④错误;
∵BC∥DE,
∴∠CBE=∠BED,
∵∠CBE=∠DAE,
∴∠AOB=∠OAE+∠AEO=60°,
∴∠AOE=120°,
∵∠PBO=∠PAC,∠BOP=∠PCA,
∴△BPO∽△APC,
∴![]() ,
,
∴![]() ,
,
∵∠APB=∠CPO,
∴△APB∽△CPO,
∴∠COP=∠ABP=60°,
∴∠COA=∠COE=60°,
∴OC平分∠AOE,故⑤正确;
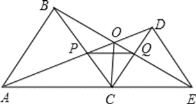
故答案为:①②③⑤.


科目:初中数学 来源: 题型:
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60 m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
定义:有三个内角相等的四边形叫“和谐四边形”.
(1)在“和谐四边形”![]() 中,若
中,若![]() ,则
,则![]() ;
;
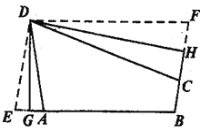
(2)如图,折叠平行四边形纸片![]() ,使顶点
,使顶点![]() ,
,![]() 分别落在边
分别落在边![]() ,
,![]() 上的点
上的点![]() ,
,![]() 处,折痕分别为
处,折痕分别为![]() ,
,![]() .
.
求证:四边形![]() 是“和谐四边形”.
是“和谐四边形”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,射线OM平分∠AOC,ON平分∠BOC.

(1)如果∠BOC=30°,求∠MON的度数;
(2)如果∠AOB=α,∠BOC=30°,其他条件不变,求∠MON的度数;
查看答案和解析>>
科目:初中数学 来源: 题型:
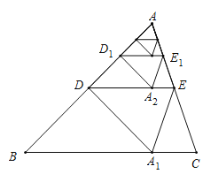
【题目】如图,将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() ,称为第
,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;还原纸片后,再将
;还原纸片后,再将![]() 沿着过
沿着过![]() 中点
中点![]() 的直线折叠,使点
的直线折叠,使点![]() 落在
落在![]() 边上的
边上的![]() 处,称为第
处,称为第![]() 次操作,折痕
次操作,折痕![]() 到
到![]() 的距离记为
的距离记为![]() ;按上述方法不断操作下去…,经过第
;按上述方法不断操作下去…,经过第![]() 次操作后得到的折痕
次操作后得到的折痕![]() ,到
,到![]() 的距离记为
的距离记为![]() ,若
,若![]() ,则
,则![]() 的值为( )
的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,滑动调节式遮阳伞的立柱![]() 垂直于地面
垂直于地面![]() ,
,![]() 为立柱上的滑动调节点,伞体的截面示意图为
为立柱上的滑动调节点,伞体的截面示意图为![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,![]() ,
,![]() ,
,![]() .当点
.当点![]() 位于初始位置
位于初始位置![]() 时,点
时,点![]() 与
与![]() 重合(图2).根据生活经验,当太阳光线与
重合(图2).根据生活经验,当太阳光线与![]() 垂直时,遮阳效果最佳.
垂直时,遮阳效果最佳.
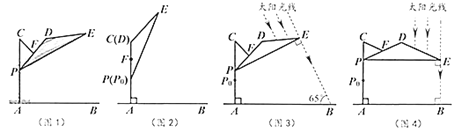
(1)上午10:00时,太阳光线与地面的夹角为![]() (图3),为使遮阳效果最佳,点
(图3),为使遮阳效果最佳,点![]() 需从
需从![]() 上调多少距离?(结果精确到
上调多少距离?(结果精确到![]() )
)
(2)中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点![]() 在(1)的基础上还需上调多少距离?(结果精确到
在(1)的基础上还需上调多少距离?(结果精确到![]() )
)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在数轴上点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,点
,点![]() 表示数
表示数![]() ,
,![]() 是多项式
是多项式![]() 的一次项系数,
的一次项系数,![]() 是绝对值最小的整数,单项式
是绝对值最小的整数,单项式![]() 的次数为
的次数为![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若将数轴在点![]() 处折叠,则点
处折叠,则点![]() 与点
与点![]() 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);
(3)点![]() 开始在数轴上运动,若点
开始在数轴上运动,若点![]() 以每秒1个单位长度的速度向右运动,同时,点
以每秒1个单位长度的速度向右运动,同时,点![]() 和点
和点![]() 分别以每秒3个单位长度和2个单位长度的速度向左运动,
分别以每秒3个单位长度和2个单位长度的速度向左运动,![]() 秒钟过后,若点
秒钟过后,若点![]() 与点B之间的距离表示为
与点B之间的距离表示为![]() ,点
,点![]() 与点
与点![]() 之间的距离表示为
之间的距离表示为![]() ,则
,则![]() = ,
= , ![]() = (用含
= (用含![]() 的代数式表示);
的代数式表示);
(4)请问:AB+BC的值是否随着时间![]() 的变化而改变?若变化,请说明理由;若不变,请求其值.
的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线AB与直线CD相交于点O,OE平分![]() .
.
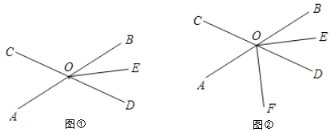
(1)如图①,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,射线OF在![]() 内部.
内部.
①若![]() ,判断OF是否为
,判断OF是否为![]() 的平分线,并说明理由;
的平分线,并说明理由;
②若OF平分![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是x=1.对于下列说法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m为实数);⑤当﹣1<x<3时,y>0,其中正确的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com