
【题目】如图,点![]() 是
是![]() 的中点,
的中点,![]() ,
,![]() ,
,![]() 平分
平分![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,四个结论中成立的是__________.
,四个结论中成立的是__________.

【答案】①②③
【解析】
过E作EF⊥AD于F,由AAS证明△AEF≌△AEB,得出BE=EF,AB=AF,∠AEF=∠AEB;证出EC=EF=BE,由HL证明Rt△EFD≌Rt△ECD,得出DC=DF,∠FED=∠CED,由平角定义得出∠AED=90°,①正确;由直角三角形的两个锐角互余得出∠ADE=∠AEB,②正确;证出AD=AF+FD=AB+DC,得出S梯形ABCD=![]() (AB+CD)BC=ADCE,③正确;只有∠ADE=30°时,AD=2AE,④不正确;即可得出结论.
(AB+CD)BC=ADCE,③正确;只有∠ADE=30°时,AD=2AE,④不正确;即可得出结论.
过E作EF⊥AD于F,如图,

∵AB⊥BC,DC⊥BC,AE平分∠BAD,
∴∠C=∠AFE=∠DFE=∠B=90°,∠FAE=∠BAE,
在△AEF和△AEB中,
 ,
,
∴△AEF≌△AEB(AAS),
∴BE=EF,AB=AF,∠AEF=∠AEB;
∵点E是BC的中点,
∴EC=EF=BE,
在Rt△EFD和Rt△ECD中,
![]() ,
,
∴Rt△EFD≌Rt△ECD(HL),
∴Rt△EFD≌Rt△ECD(HL),
∴DC=DF,∠FED=∠CED,
∵∠AEB+∠AEF+∠FED+∠CED=180°,
∴∠AED=![]() ×180°=90°,①正确;
×180°=90°,①正确;
∵EF⊥AD,
∴∠AEF=∠ADE,
∴∠ADE=∠AEB,②正确;
∵AD=AF+FD=AB+DC,S梯形ABCD=![]() (AB+CD)BC=ADCE,③正确;
(AB+CD)BC=ADCE,③正确;
只有∠ADE=30°时,AD=2AE,
∴④不正确;
故答案为:①②③


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】邮递员骑摩托车从邮局出发,先向西骑行2km到达A村,继续向西骑行3km到达B村,然后向东骑行9km到达C村,最后回到邮局.
(1)以邮局为原点,向东方向为正方向,用1cm表示1km,画出数轴,并在该数轴上表示A、B、C三个村庄的位置;
(2)C村离A村有多远?
(3)若摩托车的油耗为每千米0.03L,求邮递员这次出行的耗油量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=5,AC=12,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对垃圾进行分类投放,能有效提高对垃圾的处理和再利用,减少污染,保护环境.为了调查同学们对垃圾分类知识的了解程度,增强同学们的环保意识,普及垃圾分类及投放的相关知识,某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷,并在本校随机抽取部分同学进行问卷测试,把测试成绩分成“优、良、中、差”四个等级,绘制了如下不完整的统计图:

根据以上统计信息,解答下列问题:
(1)求成绩是“优”的人数占抽取人数的百分比;
(2)求本次随机抽取问卷测试的人数;
(3)请把条形统计图补充完整;
(4)若该校学生人数为3000人,请估计成绩是“优”和“良”的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB//CD,(1)如图,若 E 为 DC 延长线上一点,AF、CG 分别为∠BAC、∠ACE 的平分线, 求证:AF//CG.

(2)若 E 为线段 DC 上一点(E 不与 C 重合),AF、CG 分别为∠BAC、∠ACE
的平分线,画出图形,试判断 AF,CG 的位置关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“珍重生命,注意安全!”同学们在上下学途中一定要注意骑车安全.小明骑单车上学,当他骑了一段时间,想起要买某本书,于是又折回到刚经过的新华书店,买到书后继续去学校,以下是他本次所用的时间与路程的关系示意图.根据图中提供的信息回答下列问题:

(1)图中自变量是______,因变量是______;
(2)小明家到学校的路程是 米;
(3)小明在书店停留了 分钟;
(4)本次上学途中,小明一共行驶了 米,一共用了 分钟;
(5)我们认为骑单车的速度超过300米/分钟就超越了安全限度.问:在整个上学的途中哪个时间段小明骑车速度最快,速度在安全限度内吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:①(![]() 0
0![]() )-1
)-1![]() 2017
2017![]() )2018 ; ②
)2018 ; ②![]() a3b2c4)3
a3b2c4)3![]() 2)2;
2)2;
③(x+3)(x![]() )(x2
)(x2![]() ) ; ④ 19982+7992+22(用公式计算).
) ; ④ 19982+7992+22(用公式计算).
(2)(2a+b)(2ab)(a2b)2+(6a44a2)÷(2a2),其中a=![]() ,b=1.
,b=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
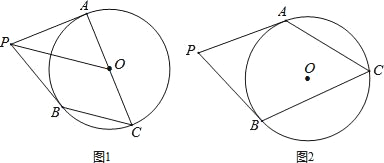
【题目】已知P为⊙O外一点,PA、PB分别切⊙O于A、B两点,点C为⊙O上一点.
(1)如图1,若AC为直径,求证:OP∥BC;
(2)如图2,若sin∠P=![]() ,求tanC的值.
,求tanC的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com