
【题目】某出租汽车公司计划购买![]() 型和
型和![]() 型两种节能汽车,若购买
型两种节能汽车,若购买![]() 型汽车
型汽车![]() 辆,
辆,![]() 型汽车
型汽车![]() 辆,共需
辆,共需![]() 万元;若购买
万元;若购买![]() 型汽车
型汽车![]() 辆,
辆,![]() 型汽车
型汽车![]() 辆,共需
辆,共需![]() 万元.
万元.
(1)![]() 型和
型和![]() 型汽车每辆的价格分别是多少万元?
型汽车每辆的价格分别是多少万元?
(2)该公司计划购买![]() 型和
型和![]() 型两种汽车共
型两种汽车共![]() 辆,费用不超过
辆,费用不超过![]() 万元,且
万元,且![]() 型汽车的数量少于
型汽车的数量少于![]() 型汽车的数量,请你给出费用最省的方案,并求出该方案所需费用.
型汽车的数量,请你给出费用最省的方案,并求出该方案所需费用.
【答案】(1)![]() 型汽车每辆的价格为
型汽车每辆的价格为![]() 万元,
万元,![]() 型汽车每辆的价格为
型汽车每辆的价格为![]() 万元;(2)费用最省的方案是购买
万元;(2)费用最省的方案是购买![]() 型汽车
型汽车![]() 辆,
辆,![]() 型汽车
型汽车![]() 辆,该方案所需费用为
辆,该方案所需费用为![]() 万元.
万元.
【解析】
(1)设![]() 型汽车每辆的价格为
型汽车每辆的价格为![]() 万元,
万元,![]() 型汽车每辆的价格为
型汽车每辆的价格为![]() 万元,根据购买
万元,根据购买![]() 型汽车
型汽车![]() 辆,
辆,![]() 型汽车
型汽车![]() 辆,共需
辆,共需![]() 万元;购买
万元;购买![]() 型汽车
型汽车![]() 辆,
辆,![]() 型汽车
型汽车![]() 辆,共需
辆,共需![]() 万元,列方程组进行求解即可;
万元,列方程组进行求解即可;
(2)设购买![]() 型汽车
型汽车![]() 辆,则购买
辆,则购买![]() 型汽车
型汽车![]() 辆,根据总费用不超过
辆,根据总费用不超过![]() 万元,且
万元,且![]() 型汽车的数量少于
型汽车的数量少于![]() 型汽车的数量,列不等式组进行求解得出购买方案,然后再讨论即可得.
型汽车的数量,列不等式组进行求解得出购买方案,然后再讨论即可得.
(1)设![]() 型汽车每辆的价格为
型汽车每辆的价格为![]() 万元,
万元,![]() 型汽车每辆的价格为
型汽车每辆的价格为![]() 万元,
万元,
由题意得:
![]() ,
,
解得![]() ,
,
答:![]() 型汽车每辆的价格为
型汽车每辆的价格为![]() 万元,
万元,![]() 型汽车每辆的价格为
型汽车每辆的价格为![]() 万元;
万元;
(2)设购买![]() 型汽车
型汽车![]() 辆,则购买
辆,则购买![]() 型汽车
型汽车![]() 辆,
辆,
由题意得:![]() ,
,
解得:![]() ,因为
,因为![]() 是整数,
是整数,
所以![]() 或
或![]() ,
,
当![]() 时,该方案所需费用为:
时,该方案所需费用为:![]() 万元;
万元;
当![]() 时,该方案所需费用为:
时,该方案所需费用为:![]() 万元,
万元,
答:费用最省的方案是购买![]() 型汽车
型汽车![]() 辆,
辆,![]() 型汽车
型汽车![]() 辆,该方案所需费用为
辆,该方案所需费用为![]() 万元.
万元.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
【题目】教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始下降,此时水温![]() (℃)与开机后用时
(℃)与开机后用时![]() (
(![]() )成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温
)成反比例关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温![]() (℃)与时间
(℃)与时间![]() (
(![]() )的关系如图所示:
)的关系如图所示:
(1)分别写出水温上升和下降阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)怡萱同学想喝高于50℃的水,请问她最多需要等待多长时间?

查看答案和解析>>
科目:初中数学 来源: 题型:
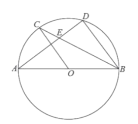
【题目】如图,![]() 为⊙
为⊙![]() 的直径,
的直径,![]() ,
,![]() 为圆上的两点,
为圆上的两点,![]() ,弦
,弦![]() ,
,![]() 相交于点
相交于点![]() ,
,
(1)求证:![]()
(2)若![]() ,
,![]() ,求⊙
,求⊙![]() 的半径;
的半径;
(3)在(2)的条件下,过点![]() 作⊙
作⊙![]() 的切线,交
的切线,交![]() 的延长线于点
的延长线于点![]() ,过点
,过点![]() 作
作![]() 交⊙
交⊙![]() 于
于![]() ,
, ![]() 两点(点
两点(点![]() 在线段
在线段![]() 上),求
上),求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
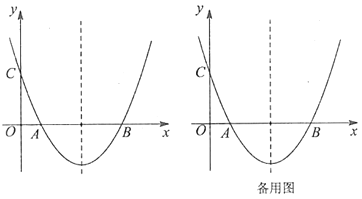
【题目】如图,抛物线![]() 经点
经点![]() ,与
,与![]() 轴相交于点
轴相交于点![]() .
.
(1)求抛物线的解析式;
(2)定义:平面上的任一点到二次函数图象上与它横坐标相同的点的距离,称为点到二次函数图象的垂直距离.如:点![]() 到二次函数图象的垂直距离是线段
到二次函数图象的垂直距离是线段![]() 的长.已知点
的长.已知点![]() 为抛物线对称轴上的一点,且在
为抛物线对称轴上的一点,且在![]() 轴上方,点
轴上方,点![]() 为平面内一点,当以
为平面内一点,当以![]() 为顶点的四边形是边长为4的菱形时,请求出点
为顶点的四边形是边长为4的菱形时,请求出点![]() 到二次函数图象的垂直距离.
到二次函数图象的垂直距离.
(3)在(2)中,当点![]() 到二次函数图象的垂直距离最小时,在
到二次函数图象的垂直距离最小时,在![]() 为顶点的菱形内部是否存在点
为顶点的菱形内部是否存在点![]() ,使得
,使得![]() 之和最小,若存在,请求出最小值;若不存在,请说明理由.
之和最小,若存在,请求出最小值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg与3.6万kg,现假定该养殖场蛋鸡产蛋量的月增长率相同.
(1)求该养殖场蛋鸡产蛋量的月平均增长率;
(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg.如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?
查看答案和解析>>
科目:初中数学 来源: 题型:
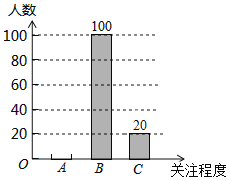
【题目】湖南省作为全国第三批启动高考综合改革的省市之一,从2018年秋季入学的高中一年级学生开始实施高考综合改革.深化高考综合改革,承载着广大考生的美好期盼,事关千家万户的切身利益,社会关注度高.为了了解我市某小区居民对此政策的关注程度,某数学兴趣小组随机采访了该小区部分居民,根据采访情况制做了如统计图表:
关注程度 | 频数 | 频率 |
A.高度关注 | m | 0.4 |
B.一般关注 | 100 | 0.5 |
C.没有关注 | 20 | n |
(1)根据上述统计图表,可得此次采访的人数为 ,m= ,n= .
(2)根据以上信息补全图中的条形统计图.
(3)请估计在该小区1500名居民中,高度关注新高考政策的约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
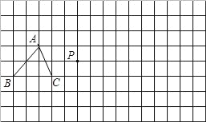
【题目】在下面16×8的正方形网格中,每个小正方形的边长为1个单位,△ABC是格点三角形(顶点在网格交点处),请你画出:
(1)△ABC关于点P的位似△A′B′C′,且位似比为1:2;
(2)以A.B.C.D为顶点的所有格点平行四边形ABCD的顶点D
.
查看答案和解析>>
科目:初中数学 来源: 题型:
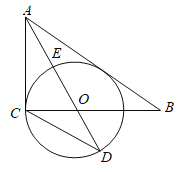
【题目】如图1,在直角△ABC中,∠ACB=90°,AO是△ABC的角平分线,以O为圆心,OC为半径作圆O
(1)求证:AB是⊙O的切线;
(2)已知AO交圆O于点E,延长AO交圆O于点D,tan∠D=![]() ,求
,求![]() 的值;
的值;
(3)如图2,在(2)条件下,若AB与⊙O的切点为点F,连接CF交AD于点G,设⊙O的半径为3,求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】类比等腰三角形的定义,我们定义:有三条边相等的凸四边形叫做“准等边四边形”
(1)已知:如图1,在“准等边四边形”ABCD中,BC≠AB,BD⊥CD,AB=3,BD=4,求BC的长;
(2)在探究性质时,小明发现一个结论:对角线互相垂直的“准等边四边形”是菱形.请你判断此结论是否正确,若正确,请说明理由;若不正确,请举出反例;
(3)如图2,在△ABC中,AB=AC,∠BAC=90°,BC=2.在AB的垂直平分线上是否存在点P使得以A,B,C,P为顶点的四边形为“准等边四边形”?若存在,请求出该“准等边四边形”的面积;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com