
【题目】在数轴上有A、B、C、D四个点,分别对应的数为a,b,c,d,且满足a,b到点 -7的距离为1 (a<b),且(c﹣12)2与|d﹣16|互为相反数.
(1)填空:a= 、b= 、c= 、d= ;
(2)若线段AB以3个单位/秒的速度向右匀速运动,同时线段CD以1单位长度/秒向左匀速运动,并设运动时间为t秒,A、B两点都运动在CD上(不与C,D两个端点重合),若BD=2AC,求t得值;
(3)在(2)的条件下,线段AB,线段CD继续运动,当点B运动到点D的右侧时,问是否存在时间t,使BC=3AD?若存在,求t得值;若不存在,说明理由.
【答案】(1)-8,-6,12,16;(2)![]() ;(3)存在,
;(3)存在,![]() 或
或![]()
【解析】
(1)根据方程与非负数的性质即可求出答案.
(2)AB、CD运动时,点A对应的数为:8+3t,点B对应的数为:6+3t,点C对应的数为:12t,点D对应的数为:16t,根据题意列出等式即可求出t的值.
(3)根据题意求出t的范围,然后根据BC=3AD求出t的值即可.
(1)∵|x+7|=1,
∴x=8或6
∴a=8,b=6,
∵(c12)2+|d16|=0,
∴c=12,d=16,
故答案为: 8;6;12;16.
(2)AB、CD运动时,
点A对应的数为:8+3t,
点B对应的数为:6+3t,
点C对应的数为:12t,
点D对应的数为:16t,
∴BD=|16t(6+3t)|=|224t|
AC=|12t(8+3t)|=|204t|
∵BD=2AC,
∴224t=±2(204t)
解得:t=![]() 或t=
或t=![]()
当t=![]() 时,此时点B对应的数为
时,此时点B对应的数为![]() ,点C对应的数为
,点C对应的数为![]() ,此时不满足题意,
,此时不满足题意,
故t=![]() ;
;
(3)当点B运动到点D的右侧时,
此时6+3t>16t
∴t>![]() ,
,
BC=|12t(6+3t)|=|184t|,
AD=|16t(8+3t)|=|244t|,
∵BC=3AD,
∴|184t|=3|244t|,
解得:t=![]() 或t=
或t=![]()
经验证,t=![]() 或t=
或t=![]() 时,BC=3AD.
时,BC=3AD.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
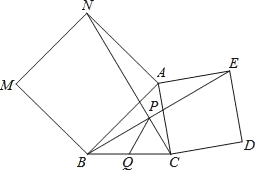
【题目】如图,分别以△ABC的两边AB和AC为边向外作正方形ANMB和正方形ACDE,NC、BE交于点P.
探究:试判断BE和CN的位置关系和数量关系,并说明理由.
应用:Q是线段BC的中点,若BC=6,则PQ= .
查看答案和解析>>
科目:初中数学 来源: 题型:
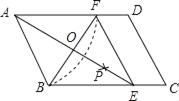
【题目】如图,在ABCD中,AB<BC,以点A为圆心,AB长为半径作圆弧交AD于点F,再分别以点B、F为圆心,大于BF的一半长为半径作圆弧,两弧交于一点P,连结AP并延长交BC于点E,连结EF.
(1)四边形ABEF是_____(填“矩形”、“菱形”、“正方形”或“无法确定”)(直接填写结果),并证明你的结论.
(2)AE、NF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为_____,∠ADC=_____°,(直接填写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
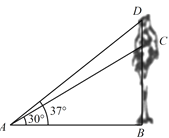
【题目】九(1)班课题学习小组,为了了解大树生长状况,去年在学校门前点 ![]() 处测得一棵大树顶点
处测得一棵大树顶点 ![]() 的仰角为
的仰角为 ![]() ,树高
,树高 ![]() .今年他们仍在原点
.今年他们仍在原点 ![]() 处测得树顶点
处测得树顶点 ![]() 的仰角为
的仰角为 ![]() ,问这棵树在这一年里生长了多少米?(结果保留两位小数,参考数据:
,问这棵树在这一年里生长了多少米?(结果保留两位小数,参考数据: ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC 的一边长为 10,另两边长分别是方程 x2 14 x 48 0 的两个根若用一圆形纸片将此三角形完全覆盖,则该圆形纸片的最小半径是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
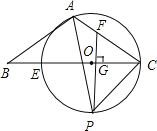
【题目】如图,在△ABC 中,AB=AC,∠BAC=120°,E 为 BC 上一点,以 CE 为直径作⊙O 恰好经过 A、C 两点, PF⊥BC 交 BC 于点 G,交 AC 于点 F.
(1)求证:AB 是⊙O 的切线;
(2)如果 CF =2,CP =3,求⊙O 的直径 EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC=60°,将一直角三角板MON的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
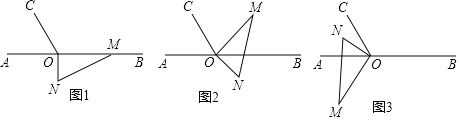
(1)求∠CON的度数;
(2)如图2是将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周的情况.在旋转的过程中,当第t秒时,三条射线OA、OC、OM构成相等的角,求此时t的值;
(3)将图1中的三角板绕点O逆时针旋转至图3,使ON在∠AOC的内部时,请探究∠AOM与∠CON的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD⊥BC于D,BD=AD,DG=DC,E,F分别是BG,AC的中点.
(1)求证:DE=DF,DE⊥DF;
(2)连接EF,若AC=10,求EF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com