
已知Rt△ABC中,AC=BC=2.一直角的顶点P在AB上滑动,
直角的两边分别交线段AC,BC于E.F两点
(1)如图1,当 =
=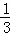 且PE⊥AC时,求证:
且PE⊥AC时,求证: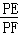 =
=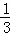 ;
;
(2)如图2,当 =1时(1)的结论是否仍然成立?
=1时(1)的结论是否仍然成立? 为什么?
为什么?
(3)在(2)的条件下,将直角∠EPF绕 点P旋转,设∠BPF=α(0°<α<90°).连
点P旋转,设∠BPF=α(0°<α<90°).连
结EF,当△CEF的周长等于2+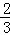
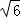 时,请直接写出α的度数.
时,请直接写出α的度数.
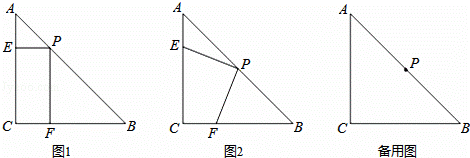
解:(1)如图1,
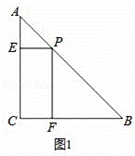

∵PE⊥AC,
∴∠AEP=∠PEC=90°.
又∵∠EPF=∠ACB=90°,
∴四边形PECF为矩形,
∴∠PFC=90°,
∴∠PFB=90°,
∴∠AEP=∠PFB.
∵AC=BC,∠C=90°,
∴∠A=∠B=45°,
∴∠FPB=∠B=45°,△AEP∽△PFB,
∴PF=BF,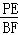 =
=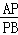 ,
,
∴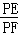 =
=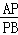 =
=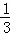 ; (3分)
; (3分)
(2)(1)的结论不成立,理由如下:
连接PC,如图2.
∵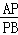 =1,
=1,
∴点P是AB的中点.
又 ∵∠ACB=90°,CA=CB,
∵∠ACB=90°,CA=CB,
∴CP=AP=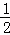 AB.∠ACP=∠BCP=
AB.∠ACP=∠BCP=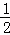 ∠ACB=45°,CP⊥AB,
∠ACB=45°,CP⊥AB,
∴∠APE+∠CPE=90°.
∵∠CPF+∠CPE=90°,
∴∠APE=∠CPF.
在△APE和△CPF中,
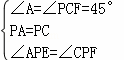 ,
,
∴△APE≌△CPF,
∴AE=CF,PE=PF.
故(1)中的结论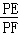 =
=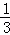 不成立; (6分)
不成立; (6分)
(3)当△CEF的周长等于2+
 时,α的度数为75°或15°.
时,α的度数为75°或15°.
提示:在(2)的条件下,可得AE=CF(已证),
∴EC+CF=EC+AE=AC=2.
∵EC+CF+EF=2+
 ,
,
∴EF=
 .
.
设CF=x,则有CE=2﹣x,
在Rt△CEF中,根据勾股定理可得x2+(2﹣x)2=(
 )2,
)2,
整理得 :3x2﹣6x+2=0,
:3x2﹣6x+2=0,
解得:x1= ,x2=
,x2=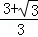 .
.
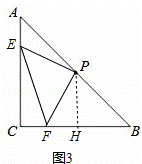
①若CF=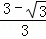 ,如图3,
,如图3,
过点P作PH⊥BC于H,
易得PH=HB=CH=1,FH=1﹣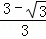 =
=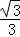 ,
,
在Rt△PHF中,tan∠FPH=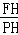 =
=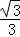 ,
,
∴∠FPH=30°,
∴α=∠FPB=30+45°=75°;  (9分)
(9分)
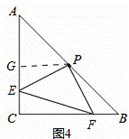
②若CF=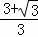 ,如图4,
,如图4,
过点P作PG⊥AC于G,
同理可得:∠APE=75°,
∴α=∠FPB=180°﹣∠APE﹣∠EPF=15°.


科目:初中数学 来源: 题型:
在ΔABC中,∠ABC的平分线与在∠ACE的平分线相交于点D。
⑴.若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数。
⑵.由⑴小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明。
查看答案和解析>>
科目:初中数学 来源: 题型:
将三角形纸片(△ABC)按如图所示的方式折叠,使点B落在边AC上,记为
点B′,折痕为EF.已知AB=AC=3,BC=4,若以点B′、F、C为顶点的三角
形与△ABC相似,则BF=_ __.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
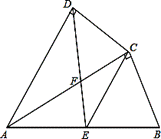
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,
E为AB中点,
 (1)求证:AC2=AB•AD;
(1)求证:AC2=AB•AD;
(2)若AD=4,AB=6,求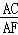 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,点P是正方形ABCD内一点,点P到点A,B和D的距离分别为1,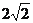 ,
, .△ADP沿点A旋转至△ABP’,连结PP’,并延长AP与BC相交于点Q.
.△ADP沿点A旋转至△ABP’,连结PP’,并延长AP与BC相交于点Q.
(1)求证:△APP’是等腰直角三角形;(2)求∠BPQ的大小;(3)求CQ 的长.
的长.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com