
(12分)数学课上林老师出示了问题:如图,AD∥BC,∠AEF=90°AD=AB=BC=DC,∠B=90°,点E是边BC的中点,且EF交∠DCG的平分线CF于点F,求证:AE=EF.
同学们作了一步又一步的研究:

(1)经过思考,小明展示了一种解题思路:如图1,取AB的中点M,连接ME,则AM=EC,易证△AME≌△ECF,所以AE=EF,小明的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(2)小颖提出一个新的想法:如图2,如果把“点E是边BC的中点”改为“点E是边BC上(除B,C外)的任意一点”,其它条件不变,那么结论“AE=EF”仍然成立,小颖的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由;
(3)小华提出:如图3,点E是BC的延长线上(除C点外)的任意一点,其他条件不变,结论“AE=EF”仍然成立.小华的观点正确吗?如果正确,写出证明过程;如果不正确,请说明理由.
见解析.
【解析】
试题分析:
试题解析:(1)正确.
∵M是AB的中点,E是BC的中点 AB=BC
∴AM=EC BM=BE ∴∠BME=45° ∠AME=135°
∵CF是∠DCG的平分线 ∴∠DCF=45° ∠ECF=135°
∴∠AME=∠ECF ∵∠AEB+∠BAE=90° ∠AEB+∠CEF=90° ∴∠BAE=∠CEF
∴△AME≌△BCF(ASA) ∴AE=EF
(2)正确.
证明:在AB上取一点M,使AM=BC,连接ME.

∴BM=BE ∴∠BME=45°∴∠AME=135°,
∵CF是∠DCG的平分线 ∴∠DCF=45° ∠ECF=135°
∴∠AME=∠ECF ∵∠AEB+∠BAE=90° ∠AEB+∠CEF=90° ∴∠BAE=∠CEF
∴△AME≌△BCF(ASA) ∴AE=EF
(3)正确.
证明:在BA的延长线上取一点N.使AN=CE,连接NE.

∴BN=BE ∠N=∠PCE=45°
∵AD∥BE ∴∠DAE=∠BAE ∴∠NAE=∠CEF ∴△ANE≌△ECF(ASA) ∴AE=EF
考点:三角形全等的证明与性质.
考点分析: 考点1:三角形 (1)三角形的概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.

 53随堂测系列答案
53随堂测系列答案科目:初中数学 来源:2014-2015学年山西农业大学附属中学八年级上学期期末考试数学试卷(解析版) 题型:选择题
要使分式 有意义,则x的取值范围是( )
有意义,则x的取值范围是( )
A、x≠1 B、x>1 C、x<1 D、x≠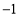
查看答案和解析>>
科目:初中数学 来源:2014-2015学年福建省七年级上学期期末考试数学试卷(解析版) 题型:选择题
把弯曲的河道改直,能够缩短航程,这样做的道理是( )

A.垂线段最短
B.两点确定一条直线
C.两点之间,线段最短
D.两点之间,直线最短
查看答案和解析>>
科目:初中数学 来源:2014-2015学年安徽省七年级下学期开学考试数学试卷(解析版) 题型:解答题
(6分)已知点C在线段AB上,且AC︰CB = 7︰13,D为CB的中点,DB = 9 cm,求AB的长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com