
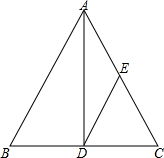
 如图,等腰△ABC中,AB=AC,AD平分∠BAC,已知AD=BC=4,且△ADE的面积等于△CDE,求DE的长度.
如图,等腰△ABC中,AB=AC,AD平分∠BAC,已知AD=BC=4,且△ADE的面积等于△CDE,求DE的长度.| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| AD2+BD2 |
| 42+22 |
| 5 |
| 5 |
| 1 |
| 2 |
| 5 |


科目:初中数学 来源: 题型:
| A、“抛一枚硬币正面朝上的概率是0.5”表示每抛硬币2次就有1次出现正面朝上 | ||
B、一次抽奖活动中,“中奖的概率是
| ||
| C、“明天降雨的概率是86%”表示明天有86%的时间降雨 | ||
| D、“刘明夺冠的可能性是98%”表示刘明夺冠的可能性很大 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
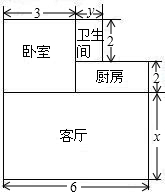 小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:
小王购买了一套经济适用房,他准备将地面铺上地砖,地面结构如图所示.根据图中的数据(单位:m),解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:
 阅读材料:
阅读材料:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com