
【题目】在平面直角坐标系xOy中,抛物线![]() 与直线
与直线![]() 交于A, B两点,其中点A在x轴上.
交于A, B两点,其中点A在x轴上.
(1)用含有b的代数式表示c;
(2)① 若点B在第一象限,且![]() ,求抛物线的解析式;
,求抛物线的解析式;
② 若![]() ,结合函数图象,直接写出b的取值范围.
,结合函数图象,直接写出b的取值范围.
【答案】(1)c=b-1;
(2)①抛物线的解析式为![]() ;②
;② ![]() 或
或![]() .
.
【解析】
(1)由题意直线y=x+1与x轴交于点A,可得出点A坐标 ,又因抛物线y=x2+bx+c经过点A,所以将点A坐标代入抛物线解析式可解得.
(2)①由y=x+1可推得∠OAC=45.
如图,已知AB=3![]() ,
, 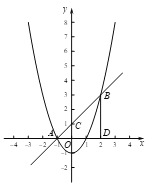
Rt△ABD中,利用勾股定理可解出AD=BD=3,所以点B的坐标为(2,3) .
将点B的坐标(2,3)代入抛物线y=x2+bx+c的解析式可得2b+c=-1.
并与(1)中得到的c=b-1联立方程组并解出方程组可得b,c的值,带入得到
抛物线的解析式.
②因为![]() ,结合函数图象,可直接得出b的取值范围.
,结合函数图象,可直接得出b的取值范围.![]() 或
或![]() .
.
解:(1)由题意直线y=x+1与x轴交于点A
可得点A坐标为(-1,0)
又因抛物线y=x2+bx+c经过点A
所以将点A坐标(-1,0)代入抛物线解析式可得
1-b+c=0,即c=b-1.
(2)①设y=x+1与y轴交于点C,可得
A (-1,0),C (0,1).
可知OA=OC=1.
又因∠AOC=90,
所以∠OAC=45.
如图,已知AB=3![]() ,过B作BD⊥x轴于点D,
,过B作BD⊥x轴于点D,

易知∠ADB=90.
又因∠BAD=45,AB=3![]() ,
,
所以AD=BD=3.
所以点B的坐标为(2,3) .
将点B的坐标(2,3)代入抛物线y=x2+bx+c的解析式可得2b+c=-1.
并与(1)中得到的c=b-1联立方程组可得:
![]() 解得
解得![]()
得抛物线的解析式为![]() .
.
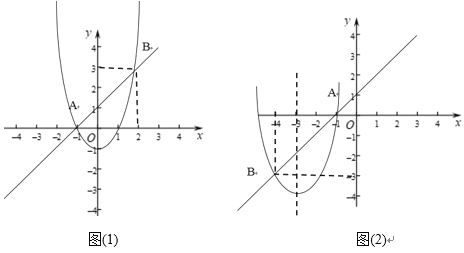
②因为![]() ,由函数图象(1)得, 对称轴
,由函数图象(1)得, 对称轴![]() 即b≤0.
即b≤0.
由函数图象(2)得, 对称轴![]() 即b≥6.
即b≥6.
所以可得出b的取值范围![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O与BC相交于点D,与CA的延长线相交于点E,过点D作DF⊥AC于点F.

(1)证明:DF是⊙O的切线;
(2)若AC=3AE,FC=6,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,△ACD沿AD折叠,使得点C落在斜边AB上的点E处.
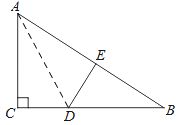
(1)求证:△BDE∽△BAC;
(2)已知AC=6,BC=8,求线段AD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]()
(1)将其化成![]() 的形式_______________;
的形式_______________;
(2)顶点坐标_________对称轴方程_______________;
(3)用五点法画出二次函数的图象;
(4) 当![]() 时,写出
时,写出![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下面题目的证明.如图,AB为⊙O的直径,AB=8,点C和点D是⊙O上关于直线AB对称的两个点,连接OC,AC,且∠BOC<90°,直线BC与直线AD相交于点E,过点C作直线CG与线段AB的延长线相交于点F,与直线AD相交于点G,且∠GAF=∠GCE
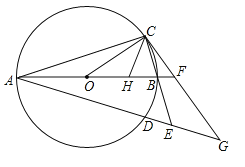
(1)求证:直线CG为⊙O的切线;
(2)若点H为线段OB上一点,连接CH,满足CB=CH;
①求证:△CBH∽△OBC;
②求OH+HC的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:一元二次方程![]() ,当
,当![]() 时,设两根为
时,设两根为![]() ,
,![]() ,则两根与系数的关系为:
,则两根与系数的关系为:![]() ;
;![]() .
.
应用:
(1)方程![]() 的两实数根分别为
的两实数根分别为![]() ,
,![]() ,则
,则![]() ______,
______,![]() _____;
_____;
(2)若关于![]() 的方程
的方程![]() 的有两个实数根
的有两个实数根![]() ,
,![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若满足![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
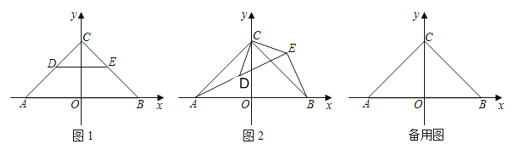
【题目】如图1,在平面直角坐标系中,点A(﹣![]() ,0),B(
,0),B(![]() ,0),C(0,
,0),C(0,![]() ).D,E分别是线段AC和CB上的点,CD=CE.将△CDE绕点C逆时针旋转一个角度α.
).D,E分别是线段AC和CB上的点,CD=CE.将△CDE绕点C逆时针旋转一个角度α.
(1)若0°<α<90°,在旋转过程中当点A,D,E在同一直线上时,连接AD,BE,如图2.求证:AD=BE,且AD⊥BE
(2)若0°<α<360°,D,E恰好是线段AC和CB上的中点,在旋转过程中,当DE∥AC时,求α的值及点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(![]() +3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距观测点D处200海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com