【题目】如图，在△ABE中，∠AEB＝90°，AE＝BE，D是AE上的一点，∠ABD＝15°，C为BE延长线上一点，且有AC＝BD，求∠ACD的度数．
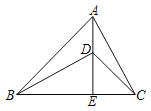
【答案】∠ACD的度数为15°．
【解析】
先由等腰三角形的性质及∠AEB=90°得出∠ABE、∠BAE、∠DBE和∠BDE的度数，再证明Rt△BDE≌Rt△ACE（HL），然后利用全等三角形的性质及等腰三角形的性质得出∠ACE和∠ECD的度数，最后利用∠ACD=∠ACE-∠ECD即可得出答案．
∵∠AEB＝90°，AE＝BE，
∴∠ABE＝∠BAE＝45°
∵∠ABD＝15°，
∴∠DBE＝30°，∠BDE＝60°
在Rt△BDE和Rt△ACE中
∴Rt△BDE≌Rt△ACE（HL）
∴ED＝EC，∠ACE＝∠BDE＝60°
∴∠EDC＝∠ECD＝45°，
∴∠ACD＝∠ACE﹣∠ECD＝60°﹣45°＝15°
答：∠ACD的度数为15°．
科目：初中数学 来源： 题型：
【题目】为积极响应市委政府“加快建设天蓝水碧地绿的美丽长沙”的号召，我市某街道决定从备选的五种树中选购一种进行栽种．为了更好地了解社情民意，工作人员在街道辖区范围内随机抽取了部分居民，进行“我最喜欢的一种树”的调查活动（每人限选其中一种树），并将调查结果整理后，绘制成如图两个不完整的统计图：
请根据所给信息解答以下问题：
（1）这次参与调查的居民人数为： ；
（2）请将条形统计图补充完整；
（3）请计算扇形统计图中“枫树”所在扇形的圆心角度数；
（4）已知该街道辖区内现有居民8万人，请你估计这8万人中最喜欢玉兰树的有多少人？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在边长为1个单位长度的小正方形组成的网格中，给出了格点△ABC（顶点是网格线的交点），在建立的平面直角坐标系中，△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1．
（1）在图中标示出旋转中心P，并写出它的坐标；
（2）以原点O为位似中心，将△A1B1C1作位似变换且放大到原来的两倍，得到△A2B2C2，在图中画出△A2B2C2，并写出C2的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，等腰△ABC的周长为21，底边BC＝5，AB的垂直平分线DE交AB于点D，交AC于点E，则△BEC的周长为（ ）
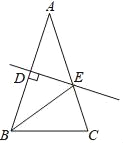
A. 13B. 16C. 8D. 10
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，方格纸中的每个小方格都是边长为1的正方形，我们把以格点间连线为边的三角形称为“格点三角形”，图中的△ABC就是格点三角形，建立如图所示的平面直角坐标系，点C的坐标为（0，﹣1）．
（1）在如图的方格纸中把△ABC以点O为位似中心扩大，使放大前后的位似比为1：2，画出△A1B1C1（△ABC与△A1B1C1在位似中心O点的两侧，A，B，C的对应点分别是A1，B1，C1）．
（2）利用方格纸标出△A1B1C1外接圆的圆心P，P点坐标是 ，⊙P的半径= ．（保留根号）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，四边形ABCD，AD∥BC，AD＝2
，BD＝BC＝3，AC＝4，将AC沿着AD方向平移至DE，使得点A与点D对应，点C与点E对应．
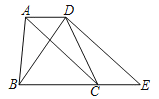
（1）猜想DE与BD的位置关系，并证明你的结论；
（2）求四边形ABCD的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店经销的某种商品，每件成本为
元．经市场调研，售价为
元时，可销售
件；售价每增加
元，销售量将减少
件．如果这种商品全部销售完，那么该商店可盈利
元．问：该商店销售了这种商品多少件？每件售价多少元？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
