
【题目】如图,对折矩形纸片![]() 使
使![]() 与
与![]() 重合,得到折痕
重合,得到折痕![]() ,再把纸片展平.
,再把纸片展平.![]() 是
是![]() 上一点,将
上一点,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 的对应点
的对应点![]() 落在
落在![]() 上.若
上.若![]() ,则
,则![]() 的长是_________.
的长是_________.

科目:初中数学 来源: 题型:
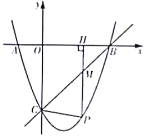
【题目】如图,若抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,直线
,直线![]() 经过点
经过点![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 下方抛物线上一动点,过点
下方抛物线上一动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() .
.
①线段![]() 是否有最大值?如果有,求出最大值;如果没有,请说明理由;
是否有最大值?如果有,求出最大值;如果没有,请说明理由;
②在点![]() 运动的过程中,是否存在点
运动的过程中,是否存在点![]() ,恰好使
,恰好使![]() 是以
是以![]() 为腰的等腰三角形?如果存在,请直接写出点
为腰的等腰三角形?如果存在,请直接写出点![]() 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校7名学生在某次测量体温(单位:℃)时得到如下数据:36.3,36.4,36.5,36.7,36.6,36.5,36.5,对这组数据描述正确的是( )
A.众数是36.5B.中位数是36.7
C.平均数是36.6D.方差是0.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
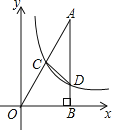
【题目】如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=![]() (x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
(x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
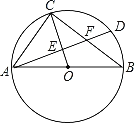
【题目】如图,△ABC内接于⊙O,AB为⊙O的直径,AB=10,AC=6,连结OC,弦AD分别交OC,BC于点E,F,其中点E是AD的中点.
(1)求证:∠CAD=∠CBA.
(2)求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批成本为每件40元的商品,若商店按单价不低于成本价,且不高于70元销售,且销售单价为正整数,经调查发现,该商品每天的销售量y(件)与销售单价x(元)之间的关系如表:
销售单价x/元 | 40 | 50 | 60 | 70 |
每天的销售量y/件 | 140 | 120 | 100 | 80 |
(1)请你认真分析表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示y与x之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式和自变量的取值范圈.
(2)销售单价定为多少元时,才能使销售该商品每天获得的利润最大?最大利润是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com