练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，将边长为8cm的正方形ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A’B’C’，当两个三角形重叠部分的面积占△ACD面积的一半时，△ABC平移的距离是______．

    【答案】4cm．

    【解析】

    根据平移的性质，结合阴影部分是平行四边形，△AA′H与△HCB′都是等腰直角三角形，则若设AA′=x，则阴影部分的底长为x，高A′D=8x，根据平行四边形的面积公式即可列出方程求解．

    解：设AC交A′B′于H，

    ∵∠A=45°，∠D=90°

    ∴△A′HA是等腰直角三角形，

    设A′H=AA′=x，则阴影部分的底长为x，高A′D=8x，

    ∵，

    ∴，

    ∴x（8-x）=16，

    解得：x=4，

    即AA′=4cm，

    ∴△ABC平移的距离是4cm；

    故答案为：4cm．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

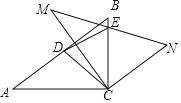
    【题目】如图，已知Rt△ABC中，∠ACB＝90°，AC＝8，BC＝6，将△ABC绕点C顺时针旋转得到△MCN，点D、E分别为AB、MN的中点，若点E刚好落在边BC上，则sin∠DEC＝__．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在平面直角坐标系中，菱形 ABCD 的边 AD∥x 轴，直线y＝2x+b 与 x 轴交于点 B，与反比例函数 y＝（k＞0）图象交于点 D 和点 E，OB＝3，OA＝4．

    （1）求反比例函数和一次函数的解析式；

    （2）点 P 为线段 BE 上的一个动点，过点 P 作 x 轴的平行线，当△CDE 被这条平行线分成面积相等的两部分时，求点 P 的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】参照学习函数的过程与方法，探究函数y=的图象与性质．

    因为y=，即y=﹣+1，所以我们对比函数y=﹣来探究．

    列表：

    x

    …

    ﹣4

    ﹣3

    ﹣2

    ﹣1

    ﹣

    1

    2

    3

    4

    …

    y=﹣

    …

    1

    2

    4

    ﹣4

    ﹣1

    1

    ﹣

    ﹣

    …

    y=

    …

    2

    3

    5

    ﹣3

    ﹣1

    0

    …

    描点：在平面直角坐标系中，以自变量x的取值为横坐标，以y=相应的函数值为纵坐标，描出相应的点，如图所示：

    （1）请把y轴左边各点和右边各点，分别用一条光滑曲线顺次连接起来；

    （2）观察图象并分析表格，回答下列问题：

    ①当x＜0时，y随x的增大而　 　；（填“增大”或“减小”）

    ②y=的图象是由y=﹣的图象向　 　平移　 　个单位而得到；

    ③图象关于点　 　中心对称．（填点的坐标）

    （3）设A（x1，y1），B（x2，y2）是函数y=的图象上的两点，且x1+x2=0，试求y1+y2+3的值．

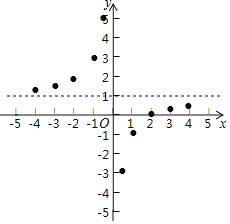
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，分别是正方形的边的中点，以为边作正方形 ，与交于点，联结．

    （1）求证：；

    （2）设，求证．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着科技的进步和网络资源的丰富，在线学习已成为更多人的自主学习选择，某校计划为学生提供以下四类在线学习方式：在线阅读、在线听课、在线答题和在线讨论，为了解学生需求，该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查，并根据调查结果绘制成如下两幅不完整的统计图．

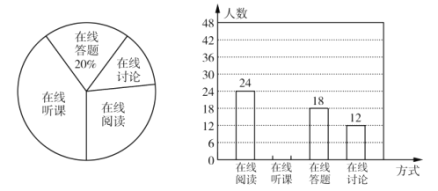
    根据图中信息，解答下列问题：

    （1）求本次调查的学生总人数，并通过计算补全条形统计图；

    （2）求扇形统计图中“在线讨论”对应的扇形圆心角的度数；

    （3）该校共有学生1800人，请你估计该校对在线阅读最感兴趣的学生人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校团委决定从4名学生会干部（小明、小华、小丽和小颖）中抽签确定2名同学去进行宣传活动，抽签规则：将4名同学姓名分别写在4张完全相同的卡片正面，把四张卡片背面朝上，洗匀后放在桌面上，既然从中随机抽取一张卡片，记下姓名，再从剩余的3张卡片中随机抽取第二张，记下姓名．试用画树状图或列表的方法表示这次抽签所有可能的结果，并求出小明被抽中的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】弹簧是一种利用弹性来工作的机械零件，用弹性材料制成的零件在外力作用下发生形变，除去外力后又恢复原状．某班同学在探究弹簧的长度与所受外力的变化关系时，通过实验记录得到的数据如下表：

    砝码的质量x（克）

    0

    50

    100

    150

    200

    250

    300

    400

    500

    指针的位置y（cm）

    2

    3

    4

    5

    6

    7

    7.5

    7.5

    7.5

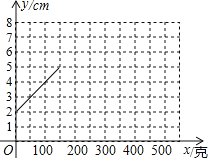
    小腾根据学习函数的经验，利用上述表格所反映出的y与x之间的变化规律，对该函数的图象与性质进行了探究，下面是小腾的探究过程，请补充完整．

    （1）根据上述表格在平面直角坐标系中补全该函数的图象；

    （2）根据画出的函数图象，写出：

    ①当x＝0时，y＝　 　，它的实际意义是　 　；

    ②当指针的位置y不变时，砝码的质量x的取值范围为　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①，直线与轴、轴分别交于两点，将沿轴正方向平移后，点、点的对应点分别为点、点，且四边形为菱形，连接，抛物线经过三点，点为上方抛物线上一动点，作，垂足为

    求此抛物线的函数关系式；

    求线段长度的最大值；

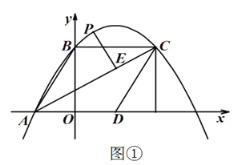
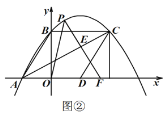
    如图②，延长交轴于点，连接，若为等腰三角形，请直接写出点的坐标．

    查看答案和解析>>

    同步练习册答案